
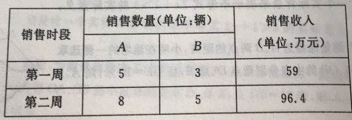
【题目】2017年12月29日郑州市人民政府通告:为减少机动车污染物排放,持续改善我市空气质量,从2018年1月1日起,每周工作日的7时至21时郑州市东三环、南三环、西三环、北三环以内区域的所有道路限行按机动车号牌(含临时号牌和外地号牌)最后一位阿拉伯数字(尾数为字母的以末尾数字为准),工作日每天限行2个号,即:号码最后一位阿拉伯数字为1和6的机动车周一限行,2和7的机动车周二限行,3和8的机动车周三限4和9的机动车周四限行,5和0的机动车周五限行,因法定节假日放假、调休而调整为上班的周六、周日按对应调体的工作日限行但通告中还规定,悬挂新能源专用牌的新能源汽车不受限制.限行通告发布后,新能源汽车成为畅销车型,某4S店销售每辆进价分别为5万元、9万元的A、B两种型号的新能源汽车,下表是近两周的销售情况:
(1)求A、B两种型号的新能源汽车的销售单价;(共
(2)若4S店准备用不超过200万元的金额采购这两种型号的新能源汽车共30辆,求B型号的新能源汽车最多能采购多少辆?
(进价、售价均保持不变,利润=销售收入一进货成本)
(3在(2)的条件下,4S销售完这230辆新能源汽车时45店的最大利润是多少?并写
【答案】(1) A型汽车的销售单价为5.8万元,B型汽车的销售单价为10万元;(2)4S店最多采购B型号的新能源汽车12辆;(3)A型号采购18辆,B型号采购12辆时,利润最大,最大利润是26.4万元.
【解析】分析: (1)设A, B两种型号的新能源汽车的销售单价分别为x元,y元,根据表格中的等量关系可得 ![]() 解得
解得![]() ,(2) 设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,根据采购两种车辆的金额不超过200万元可列不等式
,(2) 设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,根据采购两种车辆的金额不超过200万元可列不等式
10a+5.8(30-a)≤200, 解得: a≤12.5,根据实际情况取整,
(3) 设4S店销售完这30辆车,获得的利润是![]() 万元,根据总利润=A型号的销售利润+B型号的销售利润,可得:
万元,根据总利润=A型号的销售利润+B型号的销售利润,可得:![]() ,
,
详解:(1)设A, B两种型号的新能源汽车的销售单价分别为x元、y元,依题意得:
![]() 解得
解得![]()
答:A型汽车的销售单价为5.8万元,B型汽车的销售单价为10万元,
(2)设B型号的新能源汽车a辆,则采购A型号的新能源汽车 (30-a)辆,依题意得:
10a+5.8(30-a)≤200, 解得: a≤12.5. (a取整数),
答:4S店最多采购B型号的新能源汽车12辆.
(3)设4S店销售完这30辆车,获得的利润是![]() 万元,
万元,
![]() ,
,
![]() ,
,
![]() w随a的增大而增大,
w随a的增大而增大,
∴a最大时,w最大,
∵![]() ,且a是整数,
,且a是整数,
∴a=12时,w=24+0.2×12=26.4.
答:A型号采购18辆,B型号采购12辆时,利润最大,最大利润是26.4万元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y= ![]() (x>0)恰好经过点C,交AD于点E,则点E的坐标为 .
(x>0)恰好经过点C,交AD于点E,则点E的坐标为 . 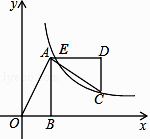
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别做出了一次函数l1和l2的图像,l1与坐标轴的交点分别为点A、点B,l1与l2的交点为点C,但被同桌小英不小心用墨水给部分污染了,我们一起来探讨
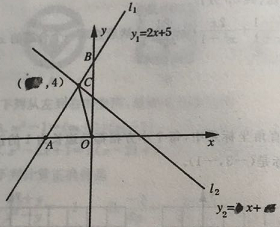
(1)写出点A、点C的坐标:A(①,0);C(②,4);
(2)求△BOC的面积:S△BOC=③
(3)直接写出不等式2x+5<·x+·的解集并回答下面问题
在解决问题(3)时,小明和小英各抒己见.小明:“l2的表达式中已经看不清楚了,并且只知道l2上一个点C的坐标,求不出该直线的表达式,所以无法求出该不等式的解集”小英说:“不用求出l2的表达式就可以得出该不等式的解集.”你同意谁的说法?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB,AB表示甲、乙两名同学运动的一次函数图象,图中s和t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:①射线AB表示甲的路程与时间的函数关系;②甲的速度比乙快1.5 m/s;③乙在甲前面12 m处起跑;④ 8 s后,甲超过了乙.其中正确的说法是( )
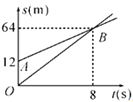
A. ①② B. ②③④ C. ②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
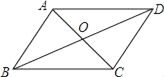
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com