
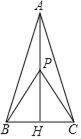
【题目】如图,△ABC中,∠BAC=30°且AB=AC,P是底边上的高AH上一点.若AP+BP+CP的最小值为2![]() ,则BC=_____.
,则BC=_____.
【答案】![]()
【解析】
如图将△ABP绕点A顺时针旋转60°得到△AMG.连接PG,CM.首先证明当M,G,P,C共线时,PA+PB+PC的值最小,最小值为线段CM的长,想办法求出AC的长即可解决问题.
如图将△ABP绕点A顺时针旋转60°得到△AMG.连接PG,CM.
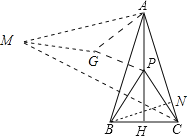
∵AB=AC,AH⊥BC,
∴∠BAP=∠CAP,
∵PA=PA,
∴△BAP≌△CAP(SAS),
∴PC=PB,
∵MG=PB,AG=AP,∠GAP=60°,
∴△GAP是等边三角形,
∴PA=PG,
∴PA+PB+PC=CP+PG+GM,
∴当M,G,P,C共线时,PA+PB+PC的值最小,最小值为线段CM的长,
∵AP+BP+CP的最小值为2![]() ,
,
∴CM=2![]() ,
,
∵∠BAM=60°,∠BAC=30°,
∴∠MAC=90°,
∴AM=AC=2,
作BN⊥AC于N.则BN=![]() AB=1,AN=
AB=1,AN=![]() ,CN=2-
,CN=2-![]() ,
,
∴BC=![]() .
.
故答案为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】点P为拋物线![]() 为常数,
为常数,![]() )上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与
)上任意一点,将抛物线绕顶点G逆时针旋转90°后得到的图象与![]() 轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
(1)抛物线![]() 的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
的对称轴是直线________,当m=2时,点P的横坐标为4时,点Q的坐标为_________;
(2)设点Q![]() 请你用含m,
请你用含m,![]() 的代数式表示
的代数式表示![]() 则
则![]() ________;
________;
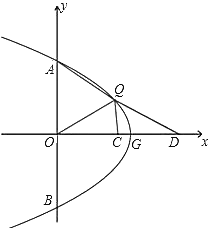
(3)如图,点Q在第一象限,点D在![]() 轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=
轴的正半轴上,点C为OD的中点,QO平分∠AQC,当AQ=2QC,QD=![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
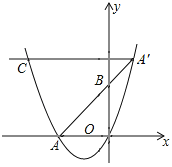
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
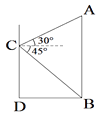
【题目】某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
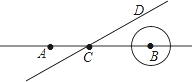
【题目】如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发________秒直线CD恰好与⊙B相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
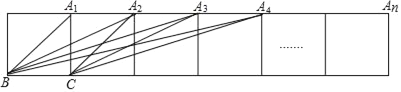
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2, 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2![]() ,则a的值为________.
,则a的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com