
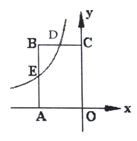
|
��ͼ��13����E��ֱ��AB��CD�ڲ�һ�㣬AB��CD������EA��ED ��1��̽�����룺 ������A=30�㣬��D=40�㣬���AED���ڶ��ٶȣ� ������A=20�㣬��D=60�㣬���AED���ڶ��ٶȣ� �۲���ͼ��13���С�AED����EAB����EDC�Ĺ�ϵ��֤����Ľ���.
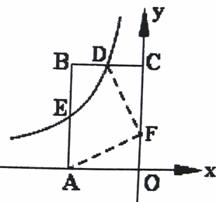
��2����չӦ�ã� ��ͼ��14��������FE�����ABCD�ı�AB���ڵ�E�����CD���ڵ�F���٢ڢֱܷۢ��DZ�����FE������4���������߽磬��������ۢ�λ��ֱ��AB�Ϸ�����P��λ�������ĸ������ϵ㣬���룺��PEB����PFC����EPF�Ĺ�ϵ����Ҫ��֤����. | |
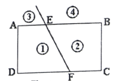
.�⣺��1���ı���ABCD�Ǿ��Σ�D��BC�е㣬
��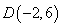
�跴������������ʽΪ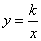
��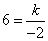 ��
��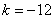
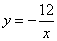
��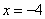 ʱ��
ʱ��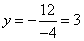
��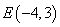
��2����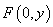
�ߡ�OAF=��DFC ��AOF�ס�FDC
��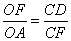 ��
��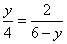
��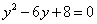
��ã�
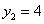
��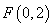 ��
��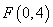
�⣺��1���١�AED=70�� �ڡ�AED=80�� �ۡ�AED=��EAB+��EDC
֤�����ӳ�AE��DC�ڵ�F��AB��DC���EAB=��EFD�֡ߡ�AED����EFD����ǡ��AED=��EDF+��EFD =��EAB+��EDC(2)P���������ʱ����EPF=3600 -(��PEB+��PFC)P���������ʱ����EPF=��PEB+��PFCP���������ʱ����EPF=��PEB-��PFCP���������ʱ����EPF=��PFC-��PFB������ֵ��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������ȫ��ͬ�Ŀ�Ƭ����A��B���飬ÿ�����ţ���A��Ŀ�Ƭ�Ϸֱ��ϡ̡��̣�B��Ŀ�Ƭ�Ϸֱ��ϡ̡�������ͼ1��ʾ��
��1��������Ƭ�ޱ�ǵ�һ�泯�ϰ������ϣ��ٷ��������鿨Ƭ���������ȡһ�ţ������ſ�Ƭ�ϱ�Ƕ��ǡ̵ĸ��ʣ���������ͼ�����б�����⣩
��2������A��B���鿨Ƭ�ޱ�ǵ�һ���Ӧճ����һ��õ�3�ſ�Ƭ��������������ͼ2��ʾ������Ƭ���泯�ϰڷ������ϣ�����ƿ�Ǹ�ס��ǡ�
��������ҿ�����һ������ �������ı���ǡ̵ĸ����Ƕ���
�������ı���ǡ̵ĸ����Ƕ���
�����ҿ����ӣ������Ŀ�Ƭ�������ǡ̺������ķ���Ҳ�ạ̇̄���¶Եĸ��ʡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����ĸ�����ͼ���У��������ĶԳ�ͼ��������Գ�ͼ�ε�ͼ���м�����

|
�鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ� ��ͼ��AB��ED��AGƽ�֡�BAC����ECF��70�㣬���FAG�Ķ�����( ) A��155�� B��145�� C��110�� D��35��
�鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ� ��֪����P(1��2a��a��2)����ԭ��ĶԳƵ��ڵ�һ�����ڣ���aΪ�����������x�ķ�ʽ���� A��5 B��1 C��3 D������ȷ�� �鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ� ��ʽ
�鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ� ��ͼ2��װ������С�ֵ��������ڡ�����¥��ʱ�IJ���ʾ��ͼ���������ּܸ�OA��OB��OC����Ϊ�߶Σ���OA=OB=OC���ҡ�AOB=120�㣬����NG-GH-HE-EF��ʾ¥�ݣ�GH��EF��ˮƽ�ߣ�NG��HE��Ǧֱ�ߣ��뾶��ȵ�С���ӡ� ��1����ͼ2�٣�����H���߶�OB�ϣ��� ��2�����һ��¥�ݵĸ߶�
�鿴�𰸺ͽ���>> ͬ����ϰ��� ����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר�� Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com��Ȩ��������վ�������£�ͼƬ��Դ�����磬����Ȩ����Ȩ��ԭ�������У�ת�������ַ���Ȩ��������Ȩ����������������֪�����ǽ����촦������ϵqq��3310059649�� ICP�������: ��ICP��07509807��-10 ����������42018502000812�� |