
【题目】某校为了解初三300名学生每天做家庭作业的时间情况,从中随机抽取50名学生进行抽样调查,按做作业的时间t(单位:小时),将学生分成四类:A类(![]() ),B类(
),B类(![]() ),C类(
),C类(![]() ),D类(
),D类(![]() ),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:

(1)补全条形统计图,并估计初三学生做作业时间为D类的学生共有多少人?
(2)抽样调查的A类学生中有3名男生和1名女生,若从中任选2人,求这2人均是男生的概率.
【答案】(1)见解析,48人;(2)![]()
【解析】
(1)由抽取的50人减去A,B,C类的人数即可求出D类人数,进而可补全条形统计图;由总人数300人乘以D类所占的百分比即可估计初三学生做作业时间为D类的学生共有得人数;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选出的2名学生中均是男生的情况,再利用概率公式即可求得答案.
解:(1)由题意可知D类的人数为:50-4-13-25=8(人),补全条形统计图如下: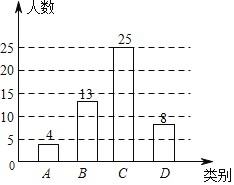
估计初三学生做作业时间为D类的学生共有![]() 人
人
(2)设3个男生分别为![]() ,
,![]() ,
,![]() ,女生为B,列如下:
,女生为B,列如下:
|
|
| B | |
| \ |
|
|
|
| p> | \ |
|
|
|
|
| \ |
|
B | B, | B, | B, | \ |
可知共有12种等可能结果,其中均是男生的有6种,
∴![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某超市计划购进甲,乙两种文具一批,已知一件甲种文具进价与一件乙种文具进价的和为![]() 元,用
元,用![]() 元购进甲种文具的件数与
元购进甲种文具的件数与![]() 元购进乙种文具的件数相同.
元购进乙种文具的件数相同.
(1)求甲乙两种文具每件进价分别是多少元;
(2)恰逢年中大促销,超市计划用不超过![]() 元资金购进甲乙两种文具共
元资金购进甲乙两种文具共![]() 件,已知卖出一件甲的利润为
件,已知卖出一件甲的利润为![]() 元,一件乙的利润为
元,一件乙的利润为![]() 元.则超市如何进货才能获得最大利润?
元.则超市如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶具店购进了A、B两种不同的茶具,1套A种茶具和2套B种茶具共需250元;3套A种茶具和4套B种茶具共需600元.
(1)求A、B两种茶具每套的进价分别是多少元?
(2)由于茶具畅销,茶具店准备再购进A、B两种茶具共80套,但这次进货时,工厂对A种茶具每套进价提高了8%,而B种茶具每套按第一次进价的八折,若茶具店本次进货总钱数不超过6240元,则最多可进A种茶具几套?
(3)若销售一套A种茶具可获利30元,销售一套B种茶其可获利20元,在(2)的条件下,如何进货可使本次购进茶具获利最多?最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
类别 | 频数(人数) | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
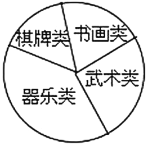
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:
①![]() ____,
____,![]() _____;
_____;
②在扇形统计图中,器乐类所对应扇形的圆心角是_____度;
③若该校七年级有学生460人,请你估计大约有多少学生参加武术类校本课程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的边BC上有一动点E,连接AE、DE,以AE、DE为边作AEDF.在点E从点B移动到点C的过程中,AEDF的面积( )

A.先变大后变小B.先变小后变大C.一直变大D.保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测绘公司借助大型无人飞机航拍测绘.如图,无人飞机从C处放飞迅速爬升到点A处,继续水平飞行400米到达B处共需150秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.己知无人飞机的水平飞行速度为4米/秒,求这架无人飞机从C到A的爬升速度及水平飞行高度.(结果保留根号)
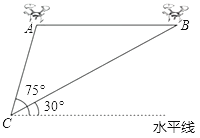
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间,我市一家服装有限公司生产了一款服装,为对比分析以前实体商店和现在网上商店两种途径的销售情况,进行了为期30天的跟踪调查.其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的关系如图所示.
为整数,单位:天)的关系如图所示.
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
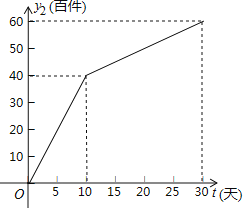
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售量
为何值时,日销售量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com