
”¾ĢāÄæ”æŹżŃ§ŠĖȤŠ”×éŃŠ¾æijŠĶŗÅĄä¹ńĪĀ¶ČµÄ±ä»ÆĒéæö£¬·¢ĻÖøĆĄä¹ńµÄ¹¤×÷¹ż³ĢŹĒ£ŗµ±ĪĀ¶Č“ļµ½Éč¶ØĪĀ¶Č![]() ”ꏱ£¬ÖĘĄäĶ£Ö¹£¬“ĖŗóĄä¹ńÖŠµÄĪĀ¶ČæŖŹ¼Öš½„ÉĻÉż£¬µ±ÉĻÉżµ½
”ꏱ£¬ÖĘĄäĶ£Ö¹£¬“ĖŗóĄä¹ńÖŠµÄĪĀ¶ČæŖŹ¼Öš½„ÉĻÉż£¬µ±ÉĻÉżµ½![]() ”ꏱ£¬ÖĘĄäæŖŹ¼£¬ĪĀ¶ČæŖŹ¼Öš½„ĻĀ½µ£¬µ±Ąä¹ń×Ō¶ÆÖĘĄäÖĮ
”ꏱ£¬ÖĘĄäæŖŹ¼£¬ĪĀ¶ČæŖŹ¼Öš½„ĻĀ½µ£¬µ±Ąä¹ń×Ō¶ÆÖĘĄäÖĮ![]() ”ꏱ£¬ÖĘĄäŌŁ“ĪĶ£Ö¹£¬”£¬°“ÕÕŅŌÉĻ·½Ź½Ń»·½ųŠŠ£®Ķ¬Ń§ĆĒ¼ĒĀ¼
”ꏱ£¬ÖĘĄäŌŁ“ĪĶ£Ö¹£¬”£¬°“ÕÕŅŌÉĻ·½Ź½Ń»·½ųŠŠ£®Ķ¬Ń§ĆĒ¼ĒĀ¼![]() ÄŚ9øöŹ±¼äµćĄä¹ńÖŠµÄĪĀ¶Č
ÄŚ9øöŹ±¼äµćĄä¹ńÖŠµÄĪĀ¶Č![]() £Ø”ę£©Ėꏱ¼ä
£Ø”ę£©Ėꏱ¼ä![]() ±ä»ÆĒéæö£¬ÖĘ³ÉĻĀ±ķ£ŗ
±ä»ÆĒéæö£¬ÖĘ³ÉĻĀ±ķ£ŗ
Ź±¼ä | ” | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | ” |
ĪĀ¶Č | ” |
|
|
|
|
|
|
|
|
| ” |
£Ø1£©ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµÖŠ£¬Ćč³öÉĻ±ķŹż¾Ż¶ŌÓ¦µÄµć£¬²¢»³öµ±![]() Ź±ĪĀ¶Č
Ź±ĪĀ¶Č![]() Ėꏱ¼ä
Ėꏱ¼ä![]() ±ä»ÆµÄŗÆŹżĶ¼Ļó£»
±ä»ÆµÄŗÆŹżĶ¼Ļó£»
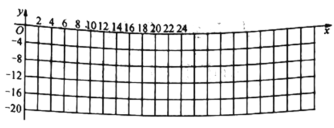
£Ø2£©ĶعżĶ¼±ķ·ÖĪö·¢ĻÖ£¬Ąä¹ńÖŠµÄĪĀ¶Č![]() ŹĒŹ±¼ä
ŹĒŹ±¼ä![]() µÄŗÆŹż£®
µÄŗÆŹż£®
¢Łµ±![]() Ź±£¬Š“³ö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½£»
Ź±£¬Š“³ö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½£»
¢Śµ±![]() Ź±£¬Š“³ö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½£»
Ź±£¬Š“³ö·ūŗĻ±ķÖŠŹż¾ŻµÄŗÆŹż½āĪöŹ½£»
£Ø3£©µ±Ē°Ąä¹ńµÄĪĀ¶Č![]() ”ꏱ£¬Ąä¹ń¼ĢŠų¹¤×÷36·ÖÖÓ£¬“ĖŹ±Ąä¹ńÖŠµÄĪĀ¶ČŹĒ¶ąÉŁ£æ
”ꏱ£¬Ąä¹ń¼ĢŠų¹¤×÷36·ÖÖÓ£¬“ĖŹ±Ąä¹ńÖŠµÄĪĀ¶ČŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©¼ūĻź½ā£»£Ø2£©¢Ły=![]() £»¢Śy=-4x+76£»£Ø£³£©-4”ć£®
£»¢Śy=-4x+76£»£Ø£³£©-4”ć£®
”¾½āĪö”æ
£Ø1£©øł¾Ż±ķøńÄŚČŻĆčµć”¢»Ķ¼”¢Į¬Ļß¼“æÉ£®
£Ø2£©¢ŁÓÉx”¤y=£80£¬¼“æÉµĆ³öµ±4”Üx<20Ź±£¬y¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£»
¢Śøł¾Żµć£Ø20£¬-4£©”¢£Ø21£¬-8£©£¬ĄūÓĆ“ż¶ØĻµŹż·ØĒó³öy¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£¬ŌŁ“śČėĘäĖüµćµÄ×ų±źŃéÖ¤¼“æÉ£®
£Ø3£©øł¾Ż±ķøńŹż¾Ż£¬ÕŅ³öĄä¹ńµÄ¹¤×÷ÖÜĘŚĪŖ20·ÖÖÓ£¬ÓÉ“Ė¼“æÉµĆ³ö“š°ø£®
£Ø1£©ČēĶ¼ĖłŹ¾£ŗ
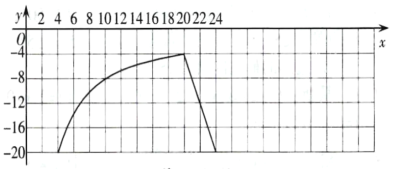
£Ø2£©¢Łøł¾ŻĶ¼ĻóæÉÖŖ£¬Ķ¼Ļó½Ó½ü·“±ČĄżŗÆŹżĶ¼ĻóµÄŅ»²æ·Ö£¬Éčy=![]() £¬¹żµć£Ø8£¬-10£©£¬
£¬¹żµć£Ø8£¬-10£©£¬
”ąk=£80£¬
”ąy=![]() £Ø4”Üx£¼20£©£®
£Ø4”Üx£¼20£©£®
¢Śøł¾ŻĶ¼ĻóæÉÖŖ£¬Ķ¼Ļó½Ó½üÖ±Ļߣ¬Éčy=kx+b£¬¹żµć£Ø20£¬-4£©£¬£Ø21£¬-8£©£¬
”ąy=-4x+76£®
£Ø£³£©”ßŅņĪĀ¶ČµÄ±ä»Æ£¬20·ÖÖÓŅ»øöÖÜĘŚ£¬
”ą36=20+16
”ąĄä¹ńĮ¬Šų¹¤×÷36·ÖÖÓŹ±£¬ŌŚ·“±ČĄżŗÆŹż±ä»Æ·¶Ī§ÄŚ£¬¹ŹĪĀ¶ČĪŖ-4”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
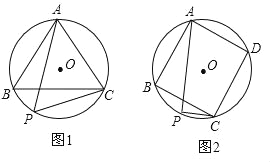
”¾ĢāÄæ”æ£Ø1£©ŅŃÖŖ£ŗČēĶ¼1£¬”÷ABCŹĒ”ŃOµÄÄŚ½ÓÕżČż½ĒŠĪ£¬µćPĪŖĮÓ»”BCÉĻŅ»¶Æµć£®ĒóÖ¤£ŗPA£½PB+PC£»
£Ø2£©ŅŃÖŖ£ŗČēĶ¼2£¬ĖıߊĪABCDŹĒ”ŃOµÄÄŚ½ÓÕż·½ŠĪ£¬µćPĪŖĮÓ»”BCÉĻŅ»¶Æµć£®ĒóÖ¤£ŗPA£½PC+![]() PB£®
PB£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
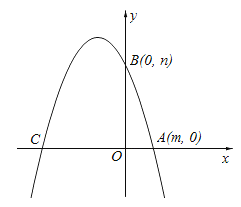
”¾ĢāÄæ”æŅŃÖŖŅ»ŌŖ¶ž“Ī·½³Ģx2©4x+3=0µÄĮ½øłŹĒm£¬nĒŅm£¼n£®ČēĶ¼£¬ČōÅ×ĪļĻßy=©x2+bx+cµÄĶ¼Ļó¾¹żµćA£Øm£¬0£©”¢B£Ø0£¬n£©£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©Čō£Ø1£©ÖŠµÄÅ×ĪļĻßÓėxÖįµÄĮķŅ»øö½»µćĪŖC£®øł¾ŻĶ¼Ļó»Ų“š£¬µ±xČ”ŗĪÖµŹ±£¬Å×ĪļĻßµÄĶ¼ĻóŌŚÖ±ĻßBCµÄÉĻ·½£æ
£Ø3£©µćPŌŚĻ߶ĪOCÉĻ£¬×÷PE”ĶxÖįÓėÅ×ĪļĻß½»ÓŚµćE£¬ČōÖ±ĻßBC½«”÷CPEµÄĆ껿·Ö³ÉĻąµČµÄĮ½²æ·Ö£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬ACĘ½·Ö”ĻDAB£¬AC2=ABAD£¬”ĻADC=90”ć£¬EĪŖABµÄÖŠµć£®

£Ø1£©ĒóÖ¤£ŗ”÷ADC”×”÷ACB£»
£Ø2£©CEÓėADÓŠŌõŃłµÄĪ»ÖĆ¹ŲĻµ£æŹŌĖµĆ÷ĄķÓÉ£»
£Ø3£©ČōAD=4£¬AB=6£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßl1£ŗy=©![]() x+1ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćAŗĶµćB£¬Ö±Ļßl2£ŗy=kx£Øk”Ł0£©ÓėÖ±Ļßl1ŌŚµŚŅ»ĻóĻŽ½»ÓŚµćC£®Čō”ĻBOC=”ĻBCO£¬ŌņkµÄÖµĪŖ£Ø””””£©
x+1ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćAŗĶµćB£¬Ö±Ļßl2£ŗy=kx£Øk”Ł0£©ÓėÖ±Ļßl1ŌŚµŚŅ»ĻóĻŽ½»ÓŚµćC£®Čō”ĻBOC=”ĻBCO£¬ŌņkµÄÖµĪŖ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ACBÖŠ£¬”ĻACB=90”ć£¬ŅŌµćAĪŖŌ²ŠÄ£¬AC³¤ĪŖ°ė¾¶µÄŌ²½»ABÓŚµćD£¬BAµÄŃÓ³¤Ļß½»”ŃAÓŚµćE£¬Į¬½ÓCE£¬CD£¬FŹĒ”ŃAÉĻŅ»µć£¬µćFÓėµćCĪ»ÓŚBEĮ½²ą£¬ĒŅ”ĻFAB=”ĻABC£¬Į¬½ÓBF£®
£Ø1£©ĒóÖ¤£ŗ”ĻBCD=”ĻBEC£»
£Ø2£©ČōBC=2£¬BD=1£¬ĒóCEµÄ³¤¼°sin”ĻABFµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
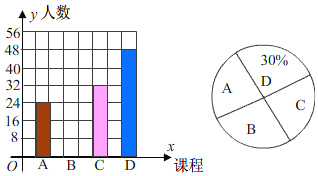
”¾ĢāÄæ”æĪŖÉī»ÆæĪ³ĢøÄøļ£¬Ä³Š£ĪŖѧɜæŖÉčĮĖŠĪŹ½¶ąŃłµÄÉēĶÅæĪ³Ģ£¬ĪŖĮĖ½ā²æ·ÖÉēĶÅæĪ³ĢŌŚŃ§ÉśÖŠ×īŹÜ»¶ÓµÄ³Ģ¶Č£¬Ń§Š£Ė껜³éČ”ĘßÄź¼¶²æ·Öѧɜ½ųŠŠµ÷²é£¬“ÓA£ŗĪÄѧĒ©ÉĶ£¬B£ŗæĘѧĢ½¾æ£¬C£ŗĪÄŹ·ĢģµŲ£¬D£ŗȤĪ¶ŹżŃ§ĖÄĆÅæĪ³ĢÖŠŃ”³öÄćĻ²»¶µÄæĪ³Ģ£Ø±»µ÷²éÕßĻŽŃ”Ņ»Ļī£©£¬²¢½«µ÷²é½į¹ū»ęÖĘ³ÉĮ½øö²»ĶźÕūµÄĶ³¼ĘĶ¼£¬ČēĶ¼ĖłŹ¾£¬øł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“Īµ÷²éµÄ×ÜČĖŹżĪŖ¶ąÉŁČĖ£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠA²æ·ÖµÄŌ²ŠÄ½ĒŹĒ¶ąÉŁ¶Č£®
£Ø2£©Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£®
£Ø3£©øł¾Ż±¾“Īµ÷²é£¬øĆŠ£ĘßÄź¼¶840Ćūѧɜ֊£¬¹Ą¼Ę×īĻ²»¶”°æĘѧĢ½¾æ”±µÄѧɜČĖŹżĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬BCŹĒĻŅ£¬”ĻB=30”ć£¬ŃÓ³¤BAµ½D£¬Ź¹”ĻBDC=30”ć£®
(1)ĒóÖ¤£ŗDCŹĒ”ŃOµÄĒŠĻߣ»
(2)ČōAB=2£¬ĒóDCµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com