
【题目】给出如下定义:对于⊙O的弦MN和⊙O外一点P(M,O,N三点不共线,且点P,O在直线MN的异侧),当∠MPN+∠MON=180°时,则称点P是线段MN关于点O的关联点.图1是点P为线段MN关于点O的关联点的示意图.
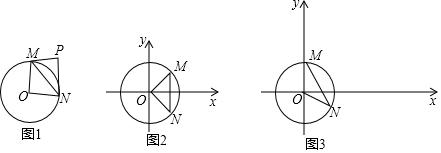
在平面直角坐标系xOy中,⊙O的半径为1.
(1)如图2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三点中,是线段MN关于点O的关联点的是 ;
,0)三点中,是线段MN关于点O的关联点的是 ;
(2)如图3,M(0,1),N(![]() ,﹣
,﹣![]() ),点D是线段MN关于点O的关联点.
),点D是线段MN关于点O的关联点.
①∠MDN的大小为 ;
②在第一象限内有一点E(![]() m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
m,m),点E是线段MN关于点O的关联点,判断△MNE的形状,并直接写出点E的坐标;
③点F在直线y=﹣![]() x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
x+2上,当∠MFN≥∠MDN时,求点F的横坐标x的取值范围.
【答案】(1)C;(2)①60;②E(![]() ,1);③点F的横坐标x的取值范围
,1);③点F的横坐标x的取值范围![]() ≤xF≤
≤xF≤![]() .
.
【解析】
(1)由题意线段MN关于点O的关联点的是以线段MN的中点为圆心,![]() 为半径的圆上,所以点C满足条件;
为半径的圆上,所以点C满足条件;
(2)①如图3-1中,作NH⊥x轴于H.求出∠MON的大小即可解决问题;
②如图3-2中,结论:△MNE是等边三角形.由∠MON+∠MEN=180°,推出M、O、N、E四点共圆,可得∠MNE=∠MOE=60°,由此即可解决问题;
③如图3-3中,由②可知,△MNE是等边三角形,作△MNE的外接圆⊙O′,首先证明点E在直线y=-![]() x+2上,设直线交⊙O′于E、F,可得F(
x+2上,设直线交⊙O′于E、F,可得F(![]() ,
,![]() ),观察图形即可解决问题;
),观察图形即可解决问题;
(1)由题意线段MN关于点O的关联点的是以线段MN的中点为圆心,![]() 为半径的圆上,所以点C满足条件,
为半径的圆上,所以点C满足条件,
故答案为C.
(2)①如图3-1中,作NH⊥x轴于H.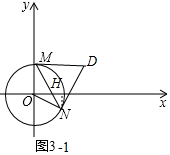
∵N(![]() ,-
,-![]() ),
),
∴tan∠NOH=![]() ,
,
∴∠NOH=30°,
∠MON=90°+30°=120°,
∵点D是线段MN关于点O的关联点,
∴∠MDN+∠MON=180°,
∴∠MDN=60°.
故答案为60°.
②如图3-2中,结论:△MNE是等边三角形.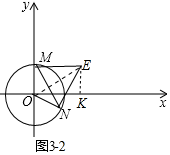
理由:作EK⊥x轴于K.
∵E(![]() ,1),
,1),
∴tan∠EOK=![]() ,
,
∴∠EOK=30°,
∴∠MOE=60°,
∵∠MON+∠MEN=180°,
∴M、O、N、E四点共圆,
∴∠MNE=∠MOE=60°,
∵∠MEN=60°,
∴∠MEN=∠MNE=∠NME=60°,
∴△MNE是等边三角形.
③如图3-3中,由②可知,△MNE是等边三角形,作△MNE的外接圆⊙O′,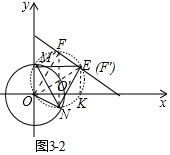
易知E(![]() ,1),
,1),
∴点E在直线y=-![]() x+2上,设直线交⊙O′于E、F,可得F(
x+2上,设直线交⊙O′于E、F,可得F(![]() ,
,![]() ),
),
观察图象可知满足条件的点F的横坐标x的取值范围![]() ≤xF≤
≤xF≤![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
【题目】某数学小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:
在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),
以AD为边在AD右侧作正方形ADEF,连接CF.
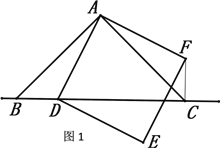
(1).如图1,当点D在线段BC上时,
①.BC与CF的位置关系为:________________________________.
②.BC,CD,CF之间的数量关系为:_______________________________.
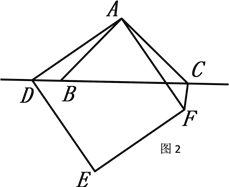
(2).如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,
请给予证明;若不成立,请你写出正确结论再给予证明.
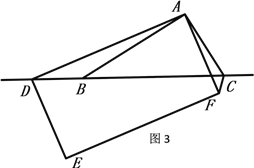
(3).如图3,将图2中的 AB=AC改变成AB=kAC,正方形ADEF改成矩形ADEF,且AD=kAF,其它条件不变 ,猜想线段BD与CF之间的关系,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
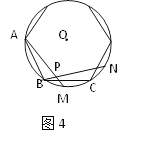
【题目】如图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
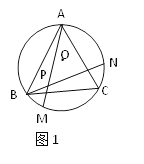
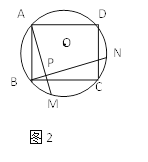

(1)求图1中∠APN的度数;
(2)图2中,∠APN的度数是_______,图3中∠APN的度数是________。
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
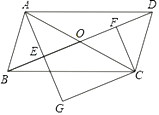
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是 ;
(2)任选两名同学打第一场,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与直线y=2x+1平行,且过点(1,﹣3).
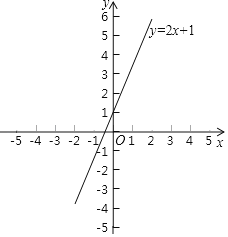
(1)求这个一次函数的关系式?
(2)画出函数图象.
(3)该函数图象与两个坐标轴围成的三角形的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
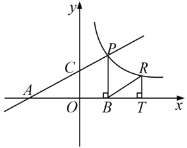
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥![]() 轴于B,且S△ABP=9.
轴于B,且S△ABP=9.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥![]() 轴于T,当△BRT与△AOC相似时,求点R的坐标.
轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com