
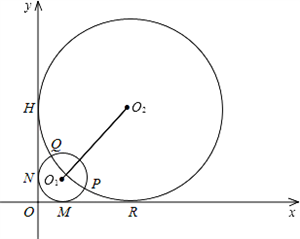
如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.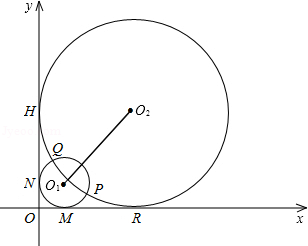
(1)求两圆的圆心O1,O2所在直线的解析式;
(2)求两圆的圆心O1,O2之间的距离d;
(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.
试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为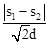 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
解:(1)由题意可知O1(m,m),O2(n,n),
设过点O1,O2的直线解析式为y=kx+b,则有: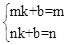 (0<m<n),解得
(0<m<n),解得 。
。
∴两圆的圆心O1,O2所在直线的解析式为:y=x。
(2)由相交两圆的性质,可知P、Q点关于O1O2对称.
∵P(4,1),直线O1O2解析式为y=x,∴Q(1,4)。
如图1,连接O1Q, O2Q。
∵Q(1,4),O1(m,m),
∴根据勾股定理得到: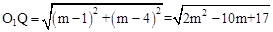 。
。
又∵O1Q为小圆半径,即QO1=m,
∴ =m,化简得:m2﹣10m+17="0" ①
=m,化简得:m2﹣10m+17="0" ①
同理可得:n2﹣10n+17="0" ②
由①,②式可知,m、n是一元二次方程x2﹣10x+17="0" ③的两个根,
解③得: 。
。
∵0<m<n,∴m=5-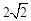 ,n=5+
,n=5+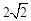 。
。
∵O1(m,m),O2(n,n),
∴d=O1O2=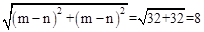 。
。
(3)不存在。理由如下:
假设存在这样的抛物线,其解析式为y=ax2+bx+c,
∵开口向下,∴a<0。
如图2,连接PQ。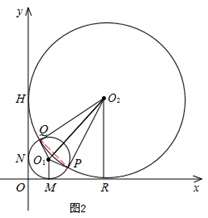
由相交两圆性质可知,PQ⊥O1O2。
∵P(4,1),Q(1,4),
∴ 。
。
又∵O1O2=8,∴ 。
。
又∵O2R=5+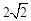 ,O1M=5-
,O1M=5-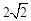 ,MR=
,MR=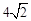 ,
,
∴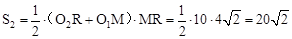
∴ ,即抛物线在x轴上截得的线段长为1。
,即抛物线在x轴上截得的线段长为1。
∵抛物线过点P(4,1),Q(1,4),
∴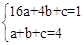 ,解得
,解得 。
。
∴抛物线解析式为:y=ax2﹣(5a+1)x+5+4a,
令y=0,则有:ax2﹣(5a+1)x+5+4a=0,
设两根为x1,x2,则有:x1+x2= ,x1x2=
,x1x2= 。
。
∵在x轴上截得的线段长为1,即|x1﹣x2|=1,
∴(x1﹣x2)2=1,∴(x1+x2)2﹣4x1x2=1,即( )2﹣4(
)2﹣4( )=1,
)=1,
化简得:8a2﹣10a+1=0,解得a=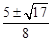 。
。
可见a的两个根均大于0,这与抛物线开口向下(即a<0)矛盾。
∴不存在这样的抛物线。
解析


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
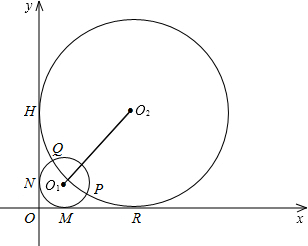 坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.| |s1-s2| | ||
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
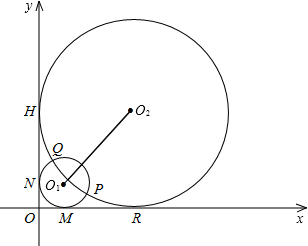 坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.
坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.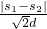 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题
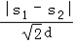
查看答案和解析>>
科目:初中数学 来源:2012年湖南省长沙市中考数学试卷(解析版) 题型:解答题
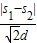 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.
的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.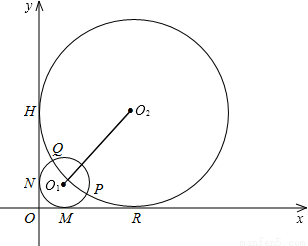
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com