
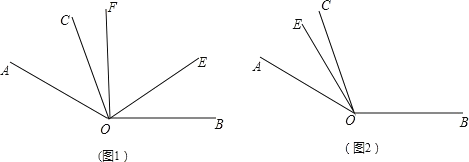
【题目】如图1,已知∠AOB=![]() ,∠AOC=
,∠AOC=![]() ,OE是∠AOB内部的一条射线,且OF平分∠AOE.
,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=![]() ,求∠COF的度数;
,求∠COF的度数;
(2)若∠COF=![]() ,求∠EOB的度数(用含n的式子表示);
,求∠EOB的度数(用含n的式子表示);
(3)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
【答案】(1)20°;(2)70°-2n°;(3)∠EOB=70°+2∠COF,理由见解析.
【解析】
(1)先求出∠AOE,再根据角平分线的定义求出∠AOF,然后根据∠COF=∠AOF-∠AOC代入数据计算即可得解;
(2)先求出∠AOF,再根据角平分线的定义求出∠AOE,然后根据∠EOB=∠AOB-∠AOE计算即可得解;
(3)设∠COF=n°,先表示出∠AOF,然后根据角平分线的定义求出∠AOE,再根据∠EOB=∠AOB-∠AOE代入计算即可得解.
解:(1)∵∠AOB=150°,∠EOB=30°,
∴∠AOE=∠AOB-∠EOB=150°-30°=120°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=
∠AOE=![]() ×120°=60°,
×120°=60°,
∴∠COF=∠AOF-∠AOC,
=60°-40°,
=20°;
(2)∵∠AOC=40°,∠COF=n°,
∴∠AOF=∠AOC+∠COF=40°+n°,
∵OF平分∠AOE,
∴∠AOE=2∠AOF=2(40°+n°)=80°+2n°,
∴∠EOB=∠AOB-∠AOE=150°-(80°+2n°)=70°-2n°;
(3)如图所示:∠EOB=70°+2∠COF.

证明:设∠COF=n°,则∠AOF=∠AOC-∠COF=40°-n°,
又∵OF平分∠AOE,
∴∠AOE=2∠AOF=80°-2n°.
∴∠EOB=∠AOB-∠AOE=150°-(80°-2n°)=(70+2n)°
即∠EOB=70°+2∠COF.


科目:初中数学 来源: 题型:
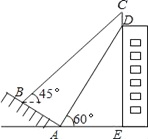
【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,然后沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: ![]() (斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(斜坡的铅直高度与水平宽度的比),经过测量AB=10米,AE=15米.
(1)求点B到地面的距离;
(2)求这块宣传牌CD的高度.(测角器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
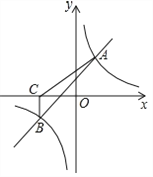
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
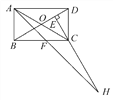
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF,EC交于点H,下列结论中:
①AF=FH;②BO=BF;③CA=CH;④BE=3ED.其中一定成立的是________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=24,动点P从A出发,以每秒2个单位的速度沿射线AB运动,运动时间为t秒(t>0),点M为AP的中点.
![]()
(1)当点P在线段AB上运动时.当t为多少时,AM=6.
(2)当点P在AB延长线上运动时,点N为BP的中点,求出线段MN的长度.
(3)在P点的运动过程中,点N为BP的中点,是否存在这样的t的值,使M、N、B三点中的一个点是以其余两点为端点的线段的中点,若有,请求出t的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式,例如![]() =1+
=1+![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ……这样的分式是假分式;像
……这样的分式是假分式;像![]() ,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:
,……这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式,例如:
![]()
![]()
(1)分式![]() 是 分式(填“真”或“假”);
是 分式(填“真”或“假”);
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知轮船在静水中航行的速度是m千米/时,水流的速度是a千米/时.
(1)轮船顺水航行的速度为 km/h,轮船逆流航行的速度为 km/h.
(2)若轮船顺水航行3小时,逆水航行2小时,则轮船共航行多少千米?
(3)当m=80,a=3时,则轮船共航行多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
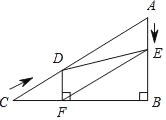
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“上”字.

(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com