
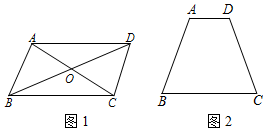
| ①AB=CD; | ②AD=BC; | ③AB∥CD; | ④AD∥BC; |
| ⑤∠BAD=∠BCD; | ⑥∠ABC=∠ADC; | ⑦OA=OC; | ⑧OB=OD. |
分析 (1)仿照小明的分类方法进行分类即可;
(2)根据小明的4种不同种类的情形,写出定理即可;
(3)利用平行四边形的定义证明即可;根据平行四边形的判定方法,即可解决问题;
(4)模仿小亮的方法,写出一些假命题,画图说明即可;
解答 (1)解:Ⅱ关于对角的2个条件可分为“⑤⑥”共1种情形;
Ⅲ关于对角线的2个条件可分为“⑦⑧”共1种情形;
Ⅳ关于边的条件与角的条件各1个可分为“①⑤,③⑤”共2种情形;
Ⅴ关于边的条件与对角线的条件各1个可分为“①⑦,③⑦”共2种情形;
Ⅵ关于角的条件与对角线的条件各1个可分为“⑤⑦,⑥⑦”共2种情形.
(2)解:定理2:两组对边分别相等的四边形是平行四边形;
定理3:一组对边平行且相等的四边形是平行四边形;
定理4:对角线互相平分的四边形是平行四边形.
故答案为:两组对边分别相等的四边形是平行四边形,一组对边平行且相等的四边形是平行四边形,对角线互相平分的四边形是平行四边形
(3)证明:∵∠BAD+∠ABC+∠BCD+∠ADC=360°,
∠BAD=∠BCD,∠ABC=∠ADC,
∴2∠BAD+2∠ABC=360°,2∠ABC+2∠BCD=360°.
∴∠BAD+∠ABC=180°,∠ABC+∠BCD=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
真命题2:四边形ABCD中,若AB∥CD,∠BAD=∠BCD,则四边形ABCD是平行四边形;
真命题3:四边形ABCD中,若AB∥CD,OA=OC,则四边形ABCD是平行四边形;
真命题4:四边形ABCD中,若∠ABC=∠ADC,OA=OC,则四边形ABCD是平行四边形;
(4)解:假命题2:四边形ABCD中,若AB=CD,∠BAD=∠BCD,则四边形ABCD不一定是平行四边形.
反例如下:如图△ABC中,AB=AC,在BC上取一点D,连接AD,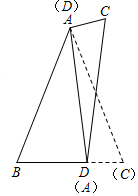
把△ADC翻转得如图所示的四边形ABDC,
∵AB=AC,∴∠B=∠C.
在四边形ABDC中,AB=CD,∠B=∠C,
显然,四边形ABDC不是平行四边形.
假命题3:四边形ABCD中,若AB=CD,OA=OC,则四边形ABCD不一定是平行四边形.
反例如下:如图,OA=OC,直线l经过点O,分别以A、C为圆心,
一定的长为半径画弧交直线l于点B、D,得如图所示的四边形ABCD,
在四边形ABCD中,AB=CD,OA=OC,
显然,四边形ABDC不是平行四边形.
假命题4:四边形ABCD中,若∠BAD=∠BCD,OA=OC,则四边形ABCD不一定是平行四边形.
反例如下:如图,筝形ABCD中,∠BAD=∠BCD,OA=OC,显然四边形ABCD不是平行四边形.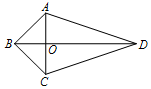
点评 本题考查四边形综合题、平行四边形的判定等知识,解题的关键是学会探究的方法,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
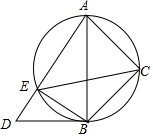 将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.
如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
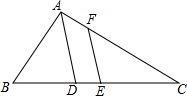 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com