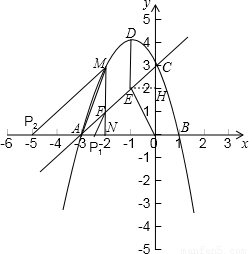
(2009•门头沟区一模)在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,且点B的坐标为(1,0),点C的坐标为(0,3).
(1)求抛物线及直线AC的解析式;
(2)E、F是线段AC上的两点,且∠AEO=∠ABC,过点F作与y轴平行的直线交抛物线于点M,交x轴于点N.当MF=DE时,在x轴上是否存在点P,使得以点P、A、F、M为顶点的四边形是梯形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q是位于抛物线对称轴左侧图象上的一点,试比较锐角∠QCO与∠BCO的大小(直接写出结果,不要求写出求解过程,但要写出此时点Q的横坐标x的取值范围).
【答案】
分析:(1)利用待定系数法,把已知坐标代入求出抛物线的解析式.设直线AC的解析式为y=kx+n,爸已知坐标代入求出直线AC的解析式.
(2)首先证明△AEO∽△ABC,利用线段比求出AE的长.然后作EH⊥y轴于H,易得E点坐标.设F点的坐标为(x,x+3),M点的坐标为(x,-x
2-2 x+3),求出点P的坐标,然后根据MP∥FA所推出的线段比求出PN的值从而求出P点坐标.
(3)份额根据x的取值范围不同求解.
解答:解:(1)∵抛物线y=-x
2+bx+c过B(1,0)、C(0,3)两点
∴
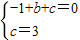
解得
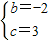
∴抛物线的解析式为y=-x
2-2x+3
由y=-x
2-2x+3可得A点坐标为(-3,0)
设直线AC的解析式为y=kx+n,
∴
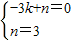
解得
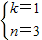
∴直线AC的解析式为y=x+3.
(2)∵OA=OC=3,OB=1
∴△AOC是等腰直角三角形,AC=
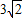
,AB=4
∴∠ECO=45°
∵∠AEO=∠ABC,∠EAO=∠BAC
∴△AEO∽△ABC
∴
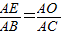
∴
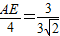
∴AE=
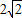
.
∴CE=AC-AE=
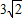
-
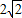
=
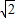
过点E作EH⊥y轴于H
可得EH=CH=1,OH=2
∴E点的坐标为(-1,2)
∵抛物线y=-x
2-2x+3顶点D的坐标为(-1,4)
∴ED=2
∴MF=ED=2
∵F在线段AC上,M在抛物线y=-x
2-2x+3上
∴设F点的坐标为(x,x+3),M点的坐标为(x,-x
2-2 x+3)
∴-x
2-2 x+3-(x+3)=2
解得x
1=-2,x
2=-1(不合题意,舍去)
∴F点的坐标为(-2,1)
∴FN=NA=1
在x轴上存在点P,使得以点P、A、F、M为顶点的四边形是梯形
当FP∥MA时,可得
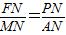
∴
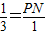
∴
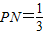
∴P点的坐标为(-

,0)
当MP∥FA时,可得
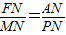
∴PN=3
∴P点的坐标为(-5,0)
∴在x轴上存在点P使得以点P、A、F、M为顶点的四边形是梯形
点P的坐标为(-

,0)或(-5,0).
(3)当x<-5时,锐角∠QCO<∠BCO
当x=-5时,锐角∠QCO=∠BCO
当-5<x<-1时,锐角∠QCO>∠BCO.
点评:本题考查的是二次函数的有关知识以及相似三角形的判定定理,难度较大.

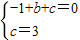
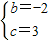
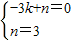
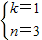
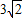 ,AB=4
,AB=4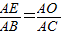
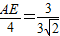
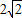 .
.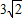 -
-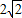 =
=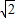
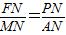

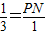
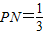
 ,0)
,0)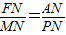
 ,0)或(-5,0).
,0)或(-5,0).

 阅读快车系列答案
阅读快车系列答案 的图象交于A(-2,1)B(1,n)两点.
的图象交于A(-2,1)B(1,n)两点.
 的图象过点A,求反比例函数的解析式.
的图象过点A,求反比例函数的解析式. ,BC=9,cos∠DAE=
,BC=9,cos∠DAE= ,求AE的长.
,求AE的长.