
【题目】已知关于x的方程(x﹣3)(x﹣2)﹣p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足 ![]() ,求实数p的值.
,求实数p的值.
【答案】
(1)
证明:(x﹣3)(x﹣2)﹣p2=0,
x2﹣5x+6﹣p2=0,
△=(﹣5)2﹣4×1×(6﹣p2)=25﹣24+4p2=1+4p2,
∵无论p取何值时,总有4p2≥0,
∴1+4p2>0,
∴无论p取何值时,方程总有两个不相等的实数根.
(2)
证明:x1+x2=5,x1x2=6﹣p2,
∵ ![]() ,
,
∴(x1+x2)2﹣2x1x2=3x1x2,
∴52=5(6﹣p2),
∴p=±1.
【解析】(1)化成一般形式,求根的判别式,当△>0时,方程总有两个不相等的实数根;
(2)根据根与系的关系求出两根和与两根积,再把 ![]() 变形,化成和与乘积的形式,代入计算,得到一个关于p的一元二次方程,解方程.
变形,化成和与乘积的形式,代入计算,得到一个关于p的一元二次方程,解方程.
本题考查了根的判别式和根与系数的关系,注意熟记以下知识点:
一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.
上面的结论反过来也成立.
一元二次方程ax2+bx+c=0(a≠0)的两实数根分别为x1 , x2 , 则有 ![]() ,
, ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( ) 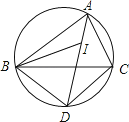
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:
①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 ![]() x2+x≥﹣
x2+x≥﹣ ![]() ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ ![]() ,
,
其中结论错误的是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,﹣3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.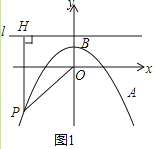
(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO= , PH= , 由此发现,POPH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,﹣2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.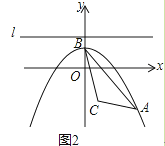
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由下列条件可判定哪两条直线平行,并说明根据.
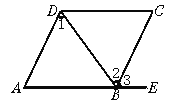
(1)∠1=∠2,________________________.
(2)∠A=∠3,________________________.
(3)∠ABC+∠C=180°,________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com