【题目】在△ABC中，AB=15，AC=13，高AD=12，则△ABC中BC边的长为（ ）
A.9
B.5
C.14
D.4或14
【答案】D
【解析】解：（1）如图，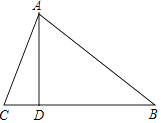 
锐角△ABC中，AC=13，AB=15，BC边上高AD=12，
∵在Rt△ACD中AC=13，AD=12，
∴CD2=AC2﹣AD2=132﹣122=25，
∴CD=5，
在Rt△ABD中AB=15，AD=12，由勾股定理得
BD2=AB2﹣AD2=152﹣122=81，
∴BD=9，
∴BC的长为BD+DC=9+5=14；
·（2）钝角△ABC中，AC=13，AB=15，BC边上高AD=12，
在Rt△ACD中AC=13，AD=12，由勾股定理得
CD2=AC2﹣AD2=132﹣122=25，
∴CD=5，
在Rt△ABD中AB=15，AD=12，由勾股定理得
BD2=AB2﹣AD2=152﹣122=81，
∴BD=9，
∴BC的长为DB﹣BC=9﹣5=4．
故选：D．
【考点精析】关于本题考查的勾股定理的概念，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
阅读快车系列答案科目：初中数学 来源： 题型：
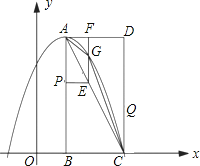
【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了准备“迎新”汇演，七（1）班学生分成甲乙两队进行几天排练.其中甲队队长对乙队队长说：你们调5人来我们队，则我们的人数和你们的人数相同；乙队队长跟甲队队长说：你们调5人来我们队，则我们的人数是你们的人数的3倍.
（1）请根据上述两位队长的交谈，求出七（1）班的学生人数；
（2）为了增强演出的舞台效果，全部学生需要租赁演出服装，班主任到某服装租赁店了解到：多于20套、少于50套服装的，可供选择的收费方式如下：
方式一：一套服装一天收取20元，另收总计80元的服装清洗费；
方式二：在一套服装一天收取20元的基础上九折，一套服装每天收取服装清洗费1元，另收每套服装磨损费5元（不按天计算）；
设租赁服装x天（x为整数），请你帮班主任参谋一下：选择那种付费方式节省一些，并说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】盛盛同学到某高校游玩时，看到运动场的宣传栏中的部分信息（如下表）：
院系篮球赛成绩公告 | |||
比赛场次 | 胜场 | 负场 | 积分 |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
盛盛同学结合学习的知识设计了如下问题，请你帮忙完成下列问题：
（1）从表中可以看出，负一场积______分,胜一场积_______分；
（2）某队在比完22场的前提下，胜场总积分能等于其负场总积分的2倍吗？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将多项式﹣a2+a3+1﹣a按字母a升幂排列正确的是（ ）
A.a3﹣a2﹣a+1
B.﹣a﹣a2+a3+1
C.1+a3﹣a2﹣a
D.1﹣a﹣a2+a3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠
是锐角，∠
是钝角，且∠
＋∠
＝180°，那么下列结论正确的是（ ）
A. ∠
的补角和∠
的补角相等 B. ∠
的余角和∠
的补角相等
C. ∠
的余角和∠
的补角互余 D. ∠
的余角和∠
的补角互补
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com