
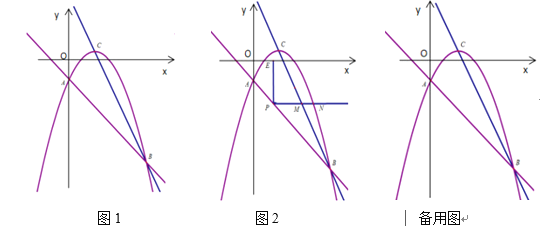
【题目】如图,直线![]() 与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为![]() .
.
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,射线![]() 轴并与直线BC和抛物线分别交于点M、N,过点P作
轴并与直线BC和抛物线分别交于点M、N,过点P作![]() 轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使
轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使![]() 的值最大,求
的值最大,求![]() 的最大值和此时Q的坐标;
的最大值和此时Q的坐标;
(3)在抛物线上找一点D,使△ABD为直角三角形,求D点的坐标.
【答案】(1)![]() ;(2)
;(2) ![]() ,Q点坐标为
,Q点坐标为![]() ;(3)
;(3) ![]() 点坐标为
点坐标为![]()
【解析】
(1)直线![]() 与抛物线分别交于点A、点B,求出点A的坐标,根据抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,求出点A的坐标,根据抛物线的顶点C的坐标为![]() .设出抛物线的解析式,把点A的坐标代入即可求出抛物线的解析式.
.设出抛物线的解析式,把点A的坐标代入即可求出抛物线的解析式.
(2) 联立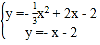 ,求出点B的坐标,用待定系数法求出BC的解析式为
,求出点B的坐标,用待定系数法求出BC的解析式为![]() ,设
,设![]() ,则
,则![]() ,进而表示出
,进而表示出![]() ,根据二次函数的性质即可求出它的最大值,此时
,根据二次函数的性质即可求出它的最大值,此时![]() ,即可求出
,即可求出![]() 的最大值以及此时Q的坐标.
的最大值以及此时Q的坐标.
(3)根据△ABD为直角三角形,分成三种情况进行讨论即可.
(1) 由题意得:![]()
![]() ,
,
设抛物线解析式为![]()
将点![]() 代入得:
代入得:![]()
解得:![]() ,
,
![]() ,
,
![]() .
.
(2) 联立 解得:
解得:![]() 或
或![]()
即![]() 点的坐标为
点的坐标为![]()
设![]() 的解析式为
的解析式为![]() ,代入
,代入![]() 和
和![]() 得:
得:

![]() 解得:
解得:![]()
∴BC的解析式为![]()
设![]() ,则
,则![]()
![]() ,
,
![]()
∴![]() ,即
,即![]()
∵C、P在y轴同侧
∴Q在PC延长线上时,![]() 最大,
最大,![]()
此时,Q为直线PC与y轴的交点,
由![]() 和
和![]() 得直线PC的解析式为:
得直线PC的解析式为:![]()
∴Q点坐标为![]()
(3) ![]() 点坐标为
点坐标为![]()


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过点(1,0)和点(0,3).
(1)求此抛物线的解析式及顶点坐标;
(2)当自变量x满足﹣1≤x≤3时,求函数值y的取值范围;
(3)将此抛物线沿x轴平移m个单位后,当自变量x满足1≤x≤5时,y的最小值为5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
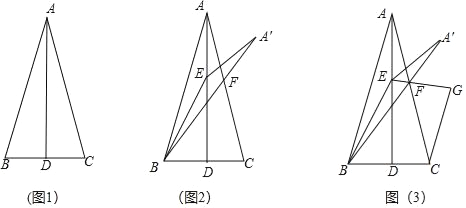
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南方旱情严重,乙水库需每天向外供相同量的水. 3天后,为缓解旱情,北方甲水库立即以管道运输的方式给乙水库送水,在给乙水库送水前甲水库的蓄水量一直为5000万m3.由于两水库相距较远,甲水库的送出的水要5天后才能到达乙水库,12天后旱情缓解,乙水库不再向外供水,甲水库也停止向乙水库送水.下图是甲水库的蓄水量与乙水库蓄水量之差y(万m3)与时间x(天)之间的函数图象.则甲水库每天的送水量为__________万m3.(假设在单位时间内,甲水库的放水量与乙水库的进水量相同,水在排放、接收以及输送过程中的损耗不计).
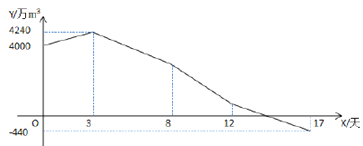
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB 是⊙O 的直径,P 为 AB 延长线上的一点,PC 切⊙O 于点 C,AD⊥PC, 垂足为 D,弦 CE 平分∠ACB,交 AB 于点 F,连接 AE.
(1)求证:PC=PF;
(2)若 tan∠ABC=![]() ,AE=5
,AE=5![]() ,求线段 PC 的长.
,求线段 PC 的长.
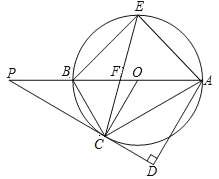
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具),以下是甲、乙两同学的作业:
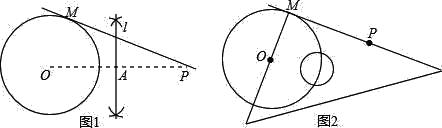
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A. 甲乙都对B. 甲乙都不对
C. 甲对,乙不对D. 甲不对,已对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
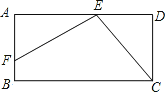
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com