
【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
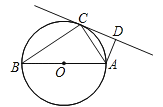
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OC,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;
(2)证明△ACB∽△ADC,得出AC2=ADAB,即可得出结果.
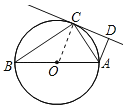
试题解析:(1)证明:连接OC,如图所示,∵AB是⊙O直径,∴∠ACB=90°,∵OB=OC,∴∠B=∠BCO,又∵∠ACD=∠B,∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,即OC⊥CD,∴CD是⊙O的切线;
(2)解:∵AD⊥CD,∴∠ADC=∠ACB=90°,又∵∠ACD=∠B,∴△ACB∽△ADC,∴AC2=ADAB=1×4=4,∴AC=2.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.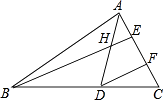
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题如图1,在边长为a的正方形中
(1)画出两个长方形阴影,则阴影部分的面积是(写成两数平方差的形式);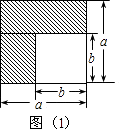
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的长是 , 宽是 , 面积是(写成多项式乘法的形式);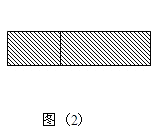
(3)比较左、右两图的阴影部分面积,可以得到乘法公式(用式子表达);
(4)运用你所得到的公式计算:
①10.3×9.7
②(2m+n﹣p)(2m﹣n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:如图,直线a,b被直线所截,若∠1+∠7=180°,则a∥b.在下面说理过程中的括号里填写说理依据.
方法一:∵∠1+∠7=180°(已知)
而∠1+∠3=180°(平角定义)
∴∠7=∠3()
∴a∥b()
方法二::∵∠1+∠7=180°(已知)
∠1+∠3=180°(平角定义)
∴∠7=∠3()
又∠7=∠6()
∴∠3=∠6()
∴a∥b()
方法三::∵∠1+∠7=180°(已知)
而∠1=∠4,∠7=∠6()
∠4+∠6=180°(平角定义)
∴a∥b()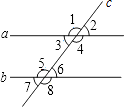
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com