
【题目】“十 一”黄金周期间,我市庐山风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)、若9月30日的游客人数记为n,请用含n的代数式表示10月2日的游客________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日;它们相差_____万人。
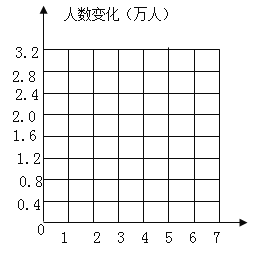
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况:
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】“国庆节大酬宾”,某商场设计的促销活动如下:在一个不透明的箱子里放有3个质地相同的小球,并在球上分别标有“5元”、“10元”和“15元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两个小球所标金额和返还相等价格的购物券,购物券可以在本商场消费,某顾客刚好消费300元.
(1)该顾客最多可得到元购物券;
(2)请你用画树状图和列表的方法,求出该顾客所得购物券的金额不低于25元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格(边长为1的小正方形组成的网格纸,正方形的顶点称为格点)是我们在初中阶段常用的工具,利用它可以解决很多问题.
(1)如图①中,△ABC是格点三角形(三个顶点为格点),则它的面积为 ;
(2)如图②,在4×4网格中作出以A为顶点,且面积最大的格点正方形(四个顶点均为格点);
(3)人们发现,记格点多边形(顶点均为格点)内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb-1,其中m,n为常数.试确定m,n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
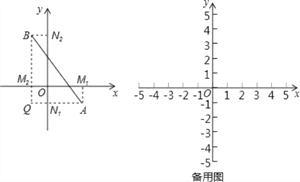
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG. 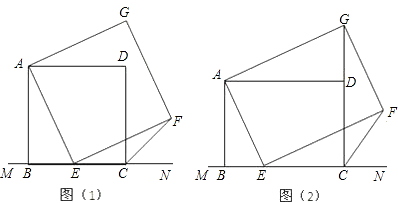
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标). 
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ![]() ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com