

 解:(1)根据圆周角定理得出:
解:(1)根据圆周角定理得出:| MH |
| NG |
| MG |
| NF |
| 1 |
| 2 |
|


科目:初中数学 来源: 题型:
 标.
标.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |


查看答案和解析>>
科目:初中数学 来源: 题型:
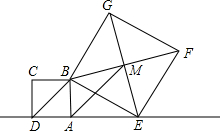 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.查看答案和解析>>
科目:初中数学 来源:2012年广东省佛山市南海区狮山镇中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com