
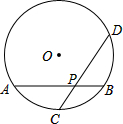
 如图,在一直径为8m的圆形戏水池中搭有两座浮桥AB,CD,已知C是
如图,在一直径为8m的圆形戏水池中搭有两座浮桥AB,CD,已知C是 |
| AB |
| 3 |
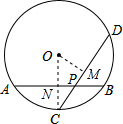 解:作OM⊥CD于点M,连接OC.
解:作OM⊥CD于点M,连接OC.| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| CM |
| OC |
2
| ||
| 4 |
| ||
| 2 |
 |
| AB |


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中有△ABC.
如图,在平面直角坐标系中有△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.
如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
1+
|
|
2+
|
|
3+
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com