
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
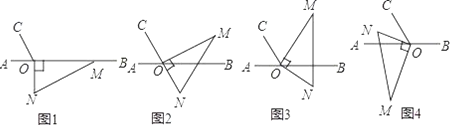
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数,∠MOB= .
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数.
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
(4)将图1中的三角尺绕点O以每秒钟15°的转速顺时针旋转一周,当时间t为 秒钟时,ON所在的直线恰好平分∠AOC.(直接写答案)
【答案】(1)30°;(2)150°;(3)30°;(4)8或20秒.
【解析】试题分析:(1)根据对顶角求出∠BON,代入∠BOM=∠MON-∠BON求出即可;
(2)求出∠BOC=120°,根据角平分线定义请求出∠COM=∠BOM=60°,代入∠CON=∠MON+∠COM求出即可;
(3)用∠AOM和∠CON表示出∠AON,然后列出方程整理即可得解.
(4))分两种情况根据旋转的性质求出旋转角,然后除以旋转速度即可得解;
试题解析:(1)如图2,∵∠AOC=60°,
∴∠BON=∠AOC=60°,
∵∠MON=90°,
∴∠BOM=∠MON-∠BON=30°;
(2)∵∠AOC=60°,
∴∠BOC=180°-∠AOC=120°,
∵OM平分∠BOC,
∴∠COM=∠BOM=60°,
∵∠MON=90°,
∴∠CON=∠MON+∠COM=90°+60°=150°;
(3)∠AOM-∠NOC=30°,
理由是:∵∠MON=90°,∠AOC=60°,
∴∠AON=90°-∠AOM,
∠AON=60°-∠NOC,
∴90°-∠AOM=60°-∠NOC,
∴∠AOM-∠NOC=30°,
故∠AOM与∠NOC之间的数量关系为:∠AOM-∠NOC=30°.
(4)直线ON恰好平分锐角∠AOC时,
旋转角为90°+30°=120°或270°+30°=300°,
∵每秒顺时针旋转15°,
∴时间为8或20秒.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
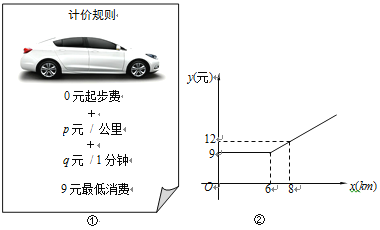
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( ) 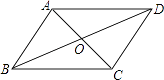
A.AB∥DC,AD=BC
B.AB∥DC,AD∥BC
C.AB=DC,AD=BC
D.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这2名学生立定跳远成绩的( )
A.方差B.平均数C.频率分布D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ BD平分∠ADC;⑤ 2∠BDC=∠BAC.其中正确的结论有 ( )
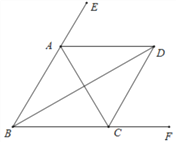
A. ①②④ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com