
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF. 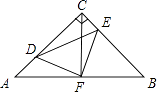
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
【答案】
(1)证明:在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中, 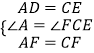 ,
,
∴△ADF≌△CEF(SAS)
(2)证明:由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形
【解析】(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(c≠4a),其图象L经过点A(-2,0).
(1)求证:b2-4ac>0;
(2)若点B(-![]() ,b+3)在图象L上,求b的值;
,b+3)在图象L上,求b的值;
(3)在(2)的条件下,若图象L的对称轴为直线x=3,且经过点C(6,-8),点D(0,n)在y轴负半轴上,直线BD与OC相交于点E,当△ODE为等腰三角形时,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
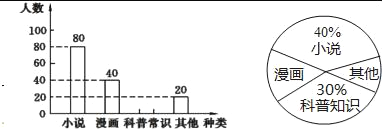
(1)这次活动一共调查了 名学生;
(2)在扇形统计图中,“其他”所在扇形的圆心角等于 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于a的方程2(a+2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ AOB=90°,且点A,B分别在反比例函数![]() (x<0),
(x<0),![]() (x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(1)求k1,k2的值;
(2)连接AB,求tan∠ OBA的值.
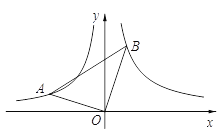
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设抛物线C1:y=x2向右平移2个单位长度,再向下平移3个单位长度得到抛物线C2 , 则抛物线C2对应的函数解析式是( )
A.y=(x﹣2)2﹣3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x+2)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/㎏) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/㎏) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300㎏,用去了1520元钱,这两种蔬菜当天全部售完一共赚了多少元钱?
(2)第二天,该经营户用1520元仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少㎏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com