
���� ��1����������ü��ϵĶ��嵱������a�Ǽ��ϵ�Ԫ��ʱ��������6-aҲ����������ϵ�Ԫ�أ������ļ������dz�Ϊ�õļ��ϣ��������֤һ�¼����жϣ�
��2������������a�Ǽ��ϵ�Ԫ��ʱ��������6-aҲ����������ϵ�Ԫ�������������дԪ���ٵļ��ϣ�
��3�������кõļ����У�Ԫ�ظ������پ���a=6-a���ɴ˼������a��Ҳ�������Ԫ�ظ������ٵļ��ϣ�
��� �⣺��1����6-1=5��5���Ǽ����е�Ԫ�أ�
�༯��{1��2}���Ǻõļ��ϣ�
��6-��-2��=8��6-1=5��6-3=3��6-5=��1��6-8=-2����8��3��5��1��-2���Ǹü��ϵ�Ԫ�أ�
�༯��{-2��1��3��5��8}��һ���õļ��ϣ�
��2������{2��4��1��5}��{3��10��-4}��
��3��Ԫ�ظ����ļ��Ͼ���ֻ��һ��Ԫ�صļ��ϣ�����Ԫ��Ϊx��
����6-x=x���ɵ�x=3��
��Ԫ�ظ������ٵļ�����{3}��
�ʴ�Ϊ�����ǣ��ǣ�{2��4��1��5}��{3��10��-4}��{3}��
���� ����������������������Ϣ�����⣬������Ŀ��Ϣ�ǽ���Ĺؼ���


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
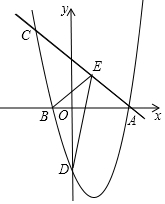 ��ͼ��������y=ax2+bx-4��a��0����x�ύ��A��4��0����B��-1��0�����㣬����A��ֱ��y=-x+4���������ڵ�C��
��ͼ��������y=ax2+bx-4��a��0����x�ύ��A��4��0����B��-1��0�����㣬����A��ֱ��y=-x+4���������ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ACΪ��O��ֱ����PA�С�O�ڵ�A����BΪ��O��һ�㣬PB��AC���ӳ��߽��ڵ�D������OB����COB=��APB������OP��
��ͼ��ACΪ��O��ֱ����PA�С�O�ڵ�A����BΪ��O��һ�㣬PB��AC���ӳ��߽��ڵ�D������OB����COB=��APB������OP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ��ֱ������ϵ�У���֪��A��0��8������B��4��0����
��ͼ��ƽ��ֱ������ϵ�У���֪��A��0��8������B��4��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
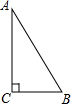 ��ͼ��Rt��ABC�У���A=30�㣬BC=2��AC=2$\sqrt{3}$����AB��Ϊ��������
��ͼ��Rt��ABC�У���A=30�㣬BC=2��AC=2$\sqrt{3}$����AB��Ϊ��������| A�� | 2 | B�� | 2$\sqrt{3}$ | C�� | 4 | D�� | 4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
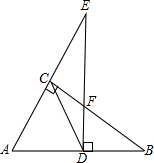 ��֪����ͼ��ʾ��CD��ֱ�ǡ�ABC��б�����ߣ�����D��ֱ��AB��ֱ�߽�BC�ڵ�F����AC���ӳ����ڵ�E����֤��CD2=DF•DE��
��֪����ͼ��ʾ��CD��ֱ�ǡ�ABC��б�����ߣ�����D��ֱ��AB��ֱ�߽�BC�ڵ�F����AC���ӳ����ڵ�E����֤��CD2=DF•DE���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com