
����Ŀ����֪����MON=40�㣬OEƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ��㣨A��B��C�����O �غϣ�������AC������OE�ڵ�D�����OAC=x�㣮 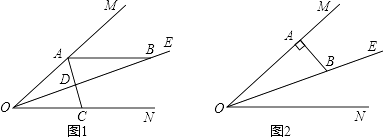
��1����ͼ1����AB��ON����
�١�ABO�Ķ�������
�ڵ���BAD=��ABDʱ��x=������BAD=��BDAʱ��x= ��
��2����ͼ2����AB��OM�����Ƿ����������x��ֵ��ʹ�á�ADB����������ȵĽǣ������ڣ����x��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��20�㣻120�㣻6��
��2���⣺�ٵ���D���߶�OB��ʱ��
����BAD=��ABD����x=20
����BAD=��BDA����x=35
����ADB=��ABD����x=50
�ڵ���D������BE��ʱ����Ϊ��ABE=110�㣬�������ε��ڽǺ�Ϊ180�㣬
����ֻ�С�BAD=��BDA����ʱx=125��
���Ͽ�֪������������x��ֵ��ʹ�á�ADB����������ȵĽǣ�
��x=20��35��50��125
���������⣺��1���١ߡ�MON=40�㣬OEƽ�֡�MON���AOB=��BON=20��
��AB��ON���ABO=20��
�ڡߡ�BAD=��ABD���BAD=20��ߡ�AOB+��ABO+��OAB=180����OAC=120��
�ߡ�BAD=��BDA����ABO=20����BAD=80��ߡ�AOB+��ABO+��OAB=180����OAC=60��
���Դ��ǣ���20 ��120��60
�����㾫��������ƽ���ߵ����ʺ������εġ����ߡ��ǽ����ĸ�������Ҫ֪����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����1�������ν�ƽ���ߵ�������ƽ���߽���һ��(�������������ڲ���������������Բ��Բ�ģ���Ϊ����);2�����������ߵ����������߽���һ��(�������������ڲ����������εļ������ģ���Ϊ����);3�������εĸ����Ƕ��㵽�Աߵľ��룻ע�⣺�����ε����ߺͽ�ƽ���߶����������ڣ�


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�����������ϵ�λ����ͼ��ʾ�����е�A��Ӧ��������Ϊ-4����AB=10������P�ӵ�A��������ÿ��2����λ���ȵ��ٶ��������������˶������˶�ʱ��Ϊt�루t>0����

��1����t=1ʱ��AP�ij�Ϊ_________����P��ʾ��������Ϊ______��
��2����PB=2ʱ����t��ֵ��
��3��MΪ�߶�AP���е㣬NΪ�߶�PB���е�. �ڵ�P�˶��Ĺ����У��߶�MN�ij����Ƿ����仯?���仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��![]() ��y��
��y��![]() �ڵ�һ�����ڵ�ͼ����ͼ����P��y��
�ڵ�һ�����ڵ�ͼ����ͼ����P��y��![]() ��ͼ����һ���㣬PC��x���ڵ�C����y��
��ͼ����һ���㣬PC��x���ڵ�C����y��![]() ��ͼ���ڵ�A. PD��y���ڵ�D����y��
��ͼ���ڵ�A. PD��y���ڵ�D����y��![]() ��ͼ���ڵ�B��.������ۣ��١�ODB���OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����CA=
��ͼ���ڵ�B��.������ۣ��١�ODB���OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����CA=![]() AP. ������ȷ������
AP. ������ȷ������

A���٢ڢ�B���٢ڢ� C���٢ۢ�D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�BC=8��AB=6��������B�͵�D��������Բ����AC���У�����AB��BC��AD��DC�ֱ��ڵ�G��H��E��F����EF+GH����Сֵ�ǣ� ��
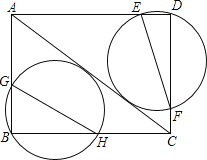
A��6 B��8 C��9.6 D��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ����MN��AC�ڵ�D����AB�ڵ�E�� 
��1������A=40�㣬���DBC�Ķ�����
��2����AE=6����CBD���ܳ�Ϊ20�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��M���߶�AC���е���N���߶�BC���е���
![]()
��1�����AC=8cm��BC=6cm����MN�ij���
��2�����AM=5cm��CN=2cm�����߶�AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е�ʽһ���������ǣ� ��
A. a2+a3=a5 B. ��a+b��2=a2+b2
C. ��2ab2��3=6a3b6 D. ��x-a����x-b��=x2-��a+b��x+ab
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x��һԪ���η��̣�k��1��x2��2x+1��0����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ�������
A.k��2��k��1B.k��2��k��0C.k��2D.k����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B���ؼ�ľ���Ϊ448ǧ�ף�һ��������Aվ������ÿСʱ��ʻ60ǧ�ף�һ�п쳵��Bվ������ÿСʱ��ʻ80ǧ�ף��ʣ�
��1������ͬʱ������������У�������ʱ��������
��2������������У������ȿ�28���ӣ���ô�쳵�����ʱ�������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com