
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,AD=5,求OC的值.
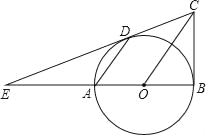
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)首选连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线;
(2)由△COD≌△COB.可得CD=CB,即可得DE=2CD,易证得△EDA∽△ECO,然后由相似三角形的对应边成比例,求得AD:OC的值.
试题解析:(1)连结DO.
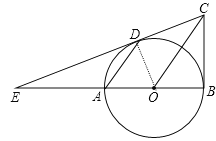
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB. 3分
又∵CO=CO, OD=OB
∴△COD≌△COB(SAS) 4分
∴∠CDO=∠CBO=90°.
又∵点D在⊙O上,
∴CD是⊙O的切线.
(2)∵△COD≌△COB.
∴CD=CB.
∵DE=2BC,
∴ED=2CD.
∵AD∥OC,
∴△EDA∽△ECO.
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
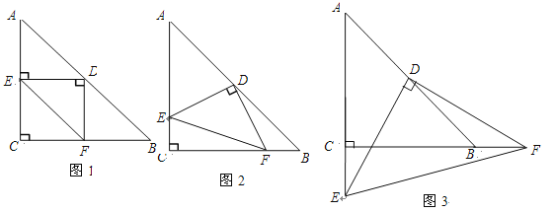
【题目】 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,
.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=8,点P为AB的中点,E为BC上一动点,过P点作FP⊥PE交AC于F点,经过P、E、F三点确定⊙O.
(1)试说明:点C也一定在⊙O上.
(2)点E在运动过程中,∠PEF的度数是否变化?若不变,求出∠PEF的度数;若变化,说明理由.
(3)求线段EF的取值范围,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
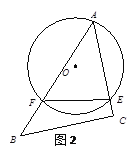
【题目】将一块含有45°的三角板ABC的顶点A放在⊙O上,且AC与⊙O相切于点A(如图1),将△ABC从点A开始,绕着点A顺时针旋转,设旋转角为α(0°<α<135°),旋转后,AC、AB分别与⊙O交于点E,F,连接EF(如图2).已知AC=8,⊙O的半径为4.
(1)在旋转过程中,有以下几个量:①弦EF的长;②![]() 的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
的长;③∠AFE的度数;④点O到EF的距离.其中不变的量是___________________(填序号);
(2)当α=________°时,BC与⊙O相切(直接写出答案);
(3)当BC与⊙O相切时,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 在坐标系中的位置如图所示,它与
在坐标系中的位置如图所示,它与![]() 轴、
轴、![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() ,点
,点![]() 是其对称轴
是其对称轴![]() 上的动点,根据图中提供的信息,给出以下结论:①
上的动点,根据图中提供的信息,给出以下结论:①![]() ;②
;②![]() 是
是![]() 的一个根;③
的一个根;③![]() 周长的最小值是
周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
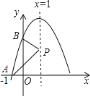
A. 仅有①② B. 仅有②③ C. 仅有①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 希望小学初一年级的![]() 名同学中,至少有两个生日相同的概率是
名同学中,至少有两个生日相同的概率是![]()
B. 在投掷骰子时,连投两次点数相同的概率与连投两次点数都为![]() 的概率相等
的概率相等
C. 我们小组共![]() 名同学,他们中肯定有两人在同一月过生日
名同学,他们中肯定有两人在同一月过生日
D. 一个游戏的中奖率是![]() ,买
,买![]() 张奖券,一定会中奖
张奖券,一定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
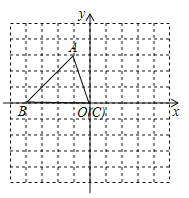
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com