
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,点A(0,1),B为y轴上一动点,以BP为边作等边△PBC.

(1)当点B运动到(0,4)时,AC= ;
(2)∠CAP的度数为 ;
(3)当点B运动时,AE的长度是否发生变化?若不变,求出AE的值;若变化,说明变化的规律.
【答案】(1)4 ;(2)60;(3)当点B运动时,AE的长度不发生变化,AE=2.
【解析】
(1)根据△AOP和△BCP是等边三角形,得到OP=AP,BP=PC,∠APO=∠CPB=60![]() ,得到∠OPB=∠APC,由此证得△PBO≌△PCA,即可得到答案;
,得到∠OPB=∠APC,由此证得△PBO≌△PCA,即可得到答案;
(2)由(1)知∠PBO=∠PCA,根据∠BAC=∠BPC=60![]() ,即可求出答案;
,即可求出答案;
(3)由∠EAO=∠BAC=60![]() ,求出∠AEO=30
,求出∠AEO=30![]() ,得到AE=2AO=2,即可得到结论.
,得到AE=2AO=2,即可得到结论.
(1)∵△AOP和△BCP是等边三角形,
∴OP=AP,BP=PC,∠APO=∠CPB=60![]() ,
,
∴∠APO+∠APB=∠BPC+∠APB,
即∠OPB=∠APC,
在△PBO和△PCA中,
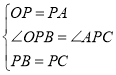 ,
,
∴△PBO≌△PCA,
∴OB=AC=4.
故答案为:4;
(2)由(1)知∠PBO=∠PCA,
∴∠BAC=∠BPC=60![]() ,
,
∵∠OAP=60![]() ,
,
∴∠CAP=180![]() -∠BAC-∠OAP=60
-∠BAC-∠OAP=60![]() .
.
故答案为:60![]() ;
;
(3)当点B运动时,AE的长度不发生变化,
理由:∵∠EAO=∠BAC=60![]() ,∠AOE=90
,∠AOE=90![]() ,
,
∴∠AEO=30![]() ,
,
∴AE=2AO=2,
即当点B运动时,AE的长度不发生变化.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知a,b是实数,定义关于“△”的一种运算如下:a△b=(a﹣b)2﹣(a+b)2.
(1)小明通过计算发现a△b=﹣4ab,请说明它成立的理由.
(2)利用以上信息得x![]() = ,若x
= ,若x![]() =3,求(x
=3,求(x![]() )4的值.
)4的值.
(3)请判断等式(a△b)△c=a△(b△c)是否成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在青海玉树地震中,大量的校舍损毁,某公司拟为灾区授建一所希望学校,甲、乙两工程队提交了投标方案,若独立完成该项目,则甲工程队所用的时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.甲、乙两队单独完成建校工程各需多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某居民小区要在一块一边靠墙(墙长![]() )的空地上修建一个矩形花园
)的空地上修建一个矩形花园![]() ,花园的一边靠墙,另三边用总长为
,花园的一边靠墙,另三边用总长为![]() 的栅栏围成.若设花园的宽为
的栅栏围成.若设花园的宽为![]() ,花园的面积为
,花园的面积为![]()
![]() .
.

![]() 求
求![]() 与
与![]() 之间的函数关系________,并写出自变量的取值范围是________;
之间的函数关系________,并写出自变量的取值范围是________;
![]() 根据
根据![]() 中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当
中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当![]() 取何值时,花园的面积最大,最大面积是多少?
取何值时,花园的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦用8万元购进纪念运动休闲衫,面市后供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种运动休闲衫时每件定价都是58元,最后剩下的150件按八折销售,很快售完.
(1)商厦第一批和第二批各购进休闲衫多少件?
(2)请问在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于点D,交AB于点E,CD=2,则AC等于( )
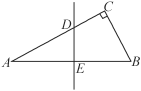
A. 4 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com