
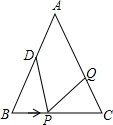
 如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.分析 (1)根据题意分别求出BP、CQ、BD、CP,根据全等三角形的判定定理证明;
(2)根据全等三角形的性质求出点P的运动时间、点Q的运动距离,计算即可.
解答 解:(1)当t=1秒时,BP=CQ=3,
∵AB=12,点D为AB的中点,
∴BD=6,
PC=9-BP=6,
∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
$\left\{\begin{array}{l}{BP=CQ}\\{∠B=∠C}\\{BD=PC}\end{array}\right.$,
∴△BPD≌△CQP;
(2)∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C,△BPD≌△CQP,
∴BP=CP=4.5,CQ=BD=6,
点P的运动时间为4.5÷3=1.5,
∴点Q的运动速度为6÷1.5=4(厘米/秒),
答:点Q的运动速度为4厘米/秒时,△BPD≌△CPQ.
点评 本题考查的是去掉三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
 某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.
某农民带了若干千克玉米进城出卖,为了方便,他带了一些零用钱备用,他先按市场价出卖一些后,又降价卖,卖出玉米千克数x与他手中持有钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 捐款额(x)元 | 户数 |
| A | 1≤x<50 | a |
| B | 50≤x<100 | 10 |
| C | 100≤x<150 | 20 |
| D | 150≤x<200 | 14 |
| E | x≥200 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com