
如图,有一个直角△ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P.Q两点分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,才能使ΔABC≌ΔPQA.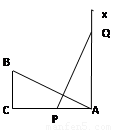
10
【解析】
试题分析:要使△ABC≌△PQA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAQ=90°,
又∵AP=CB=5,PQ=AB,
∴△ABC≌△PQA.
点P运动到C点时,△ABC≌△PQA.
∵AX⊥AC,∠C=90°,
∴∠BCA=∠QAP =90°,
又∵AP=CA=10,PQA=AB,
∴△ABC≌△PQA.
考点:直角三角形全等的判定
点评:直角三角形全等的判定和性质的应用是初中数学极为重要的知识,与各个知识点联系极为容易,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
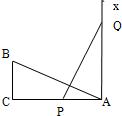 3、如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到
3、如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到查看答案和解析>>
科目:初中数学 来源: 题型:
 27、如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出BD的长吗?
27、如图,有一个直角三角形纸片,两直角边AC=18cm,BC=24cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出BD的长吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.
如图,有一个直角三角形ABC,两直角边AC=6cm,BC=8cm,AD平分∠BAC,点E在斜边AB上且AE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:
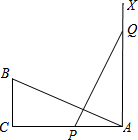 如图,有一个直角三角形ABC,∠C=90°,AC=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,且PQ=AB.问当AP=
如图,有一个直角三角形ABC,∠C=90°,AC=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,且PQ=AB.问当AP=查看答案和解析>>
科目:初中数学 来源: 题型:
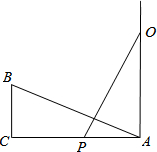 如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=5,一条线段PO=AB,P、O两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=
如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=5,一条线段PO=AB,P、O两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com