练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

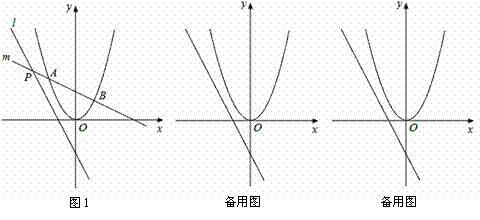
    如图1，点P是直线l：y=－2x－2上的点，过点P的另一条直线m交抛物线y=x2于A、B两点．

    （1）若A(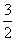－，n)、B(1，1)，求直线m的解析式；

    （2）若P(－2，t)，当PA＝AB时，求点A的坐标；

    （3）无论点P在l上移动到何处，是否总可以找到这样的直线，使得PA＝AB？若存在，请给予证明，若不存在，请说明理由．

     



    …2分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    利用二次函数的图象求一元二次方程x2＋2x－10＝3的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，已知二次函数经过、、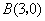C三点，点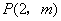是抛物线与直线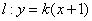的一个交点．

    （1）求二次函数关系式和点C的坐标；

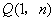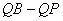    （2）对于动点，求的最大值；

    （3）若动点M在直线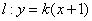上方的抛物线运动，过点M做x轴的垂线交x轴于点F，如果直线AP把线段MF分成1:2的两部分，求点M的坐标。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在□ABCD中，E、F为对角线BD上的两点，且BE＝DF． 

    求证：∠BAE＝∠DCF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：

    这些运动员跳远成绩的中位数和众数分别是

      A．190，200           B．9，9         C．15，9        D．185，200

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD中，AB＝8cm，对角线AC、BD相交于点O，  点E、F分别从B、C两点同时出发，以1cm/s的速度沿BC、CD  运动，到点C、D时停止运动，设运动时间为t(s)，△OEF的面  积为s(cm2)，则s(cm2)与t(s)的函数关系可用图像表示为

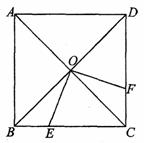
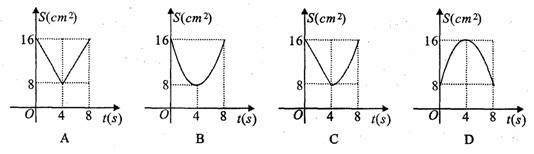
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了激发学生学习英语的兴趣，某中学举行了校园英文歌曲大赛，并设立了一、二、三等奖。学校计划根据设奖情况共买50件奖品，其中购买二等奖奖品件数比一等奖奖品件数的2倍件数还少10件，购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍，且三等奖奖品数不能少于前两种奖品数之和．其中各种奖品的单价如下表所示，如果计划一等奖奖品买x件，买50件奖品的总费用是w元．

        (1)用含有x的代数式表示：该校团委购买二等奖奖品多少件，三等奖奖品多少件？并表示w与x的函数关系式；

        (2)请问共有哪几种方案？

    (3)请你计算一下，学校应如何购买这三种奖品，才能使所支出的总费用最少，最少是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ＝       ，

    查看答案和解析>>

    同步练习册答案