练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，淇淇一家驾车从A地出发，沿着北偏东60°的方向行驶，到达B地后沿着南偏东50°的方向行驶来到C地，C地恰好位于A地正东方向上，则（　　）

    ①B地在C地的北偏西50°方向上；

    ②A地在B地的北偏西30°方向上；

    ③cos∠BAC=；

    ④∠ACB=50°．其中错误的是（　　）

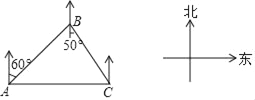
    A. ①② B. ②④ C. ①③ D. ③④

    【答案】B

    【解析】

    先根据题意画出图形，再根据平行线的性质及方向角的描述方法解答即可．

    如图所示，

    由题意可知，∠1=60°，∠4=50°，

    ∴∠5=∠4=50°，即B在C处的北偏西50°，故①正确；

    ∵∠2=60°，

    ∴∠3+∠7=180°﹣60°=120°，即A在B处的北偏西120°，故②错误；

    ∵∠1=∠2=60°，

    ∴∠BAC=30°，

    ∴cos∠BAC=，故③正确；

    ∵∠6=90°﹣∠5=40°，即公路AC和BC的夹角是40°，故④错误．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】仔细阅读下面例题，解答问题：

    例题：已知二次三项式有一个因式是，求另一个因式以及的值．

    解：设另一个因式为，得，

    则，

    ，

    解得，，

    ∴另一个因式为，的值为．

    仿照例题方法解答：

    （1）若二次三项式的一个因式为，求另一个因式；

    （2）若二次三项式有一个因式是，求另一个因式以及的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y是x的反比例函数，且当x＝2时，y＝﹣3，

    （1）求y与x之间的函数关系式；

    （2）画出这个函数的图象；

    （3）试判断点P（﹣2，3）是否在这个函数的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM=PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（　　）

    A. 4B. 3C. 2D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）

    A. 40° B. 45° C. 60° D. 70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学为了美化校园环境，计划购进桂花树和黄桷树两种树苗共200棵，现通过调查了解到：若购进15棵桂花树和6棵黄桷树共需600元，若购进12棵桂花树和5棵黄桷树共需490元．

    （1）求购进的桂花树和黄桷树的单价各是多少元？

    （2）已知甲、乙两个苗圃的两种树苗销售价格和上述价格一样，但有如下优惠：甲苗圃：每购买一棵黄桷树送两棵桂花树，购买的其它桂花树打9折．乙苗圃：购买的黄桷树和桂花树都打7折．设购买黄桷树x棵，y1和y2分别表示到甲、乙两个苗圃中购买树苗所需总费用，求出y1和y2关于x的函数表达式；

    （3）现在，学校根据实际需要购买的黄桷树的棵数不少于35棵且不超过40棵，请设计一种购买方案，使购买的树苗所花费的总费用最少．最少费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在等腰Rt△ABC中，∠BAC=90°，点E在AC上（且不与点A、C重合）．在△ABC的外部作等腰Rt△CED，使∠CED=90°，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

    （1）求证：△AEF是等腰直角三角形；

    （2）如图2，将△CED绕点C逆时针旋转，当点E在线段BC上时，连接AE，求证：AF=AE；

    （3）如图3，将△CED绕点C继续逆时针旋转，当平行四边形ABFD为菱形，且△CED在△ABC的下方时，若AB=2，CE=2，求线段AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2011山东济南，27，9分）如图，矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线经过A、C两点，与AB边交于点D．

    （1）求抛物线的函数表达式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ=CP，连接PQ，设CP=m，△CPQ的面积为S．

    ①求S关于m的函数表达式，并求出m为何值时，S取得最大值；

    ②当S最大时，在抛物线的对称轴l上若存在点F，使△FDQ为直角三角形，请直接写出所有符合条件的F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某教育局组织了“落实十九大精神，立足岗位见行动”教师演讲比赛，根据各校初赛成绩在小学组、中学组分别选出10名教师参加决赛，这些选手的决赛成绩如图所示：

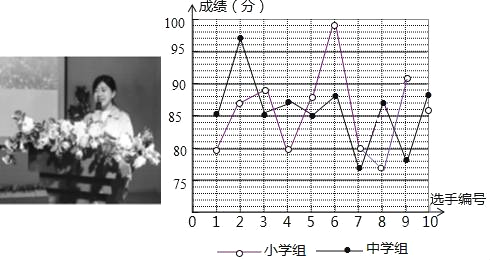
    根据上图提供的信息，回答下列问题：

    （1）请你把下面表格填写完整：

    团体成绩

    众数

    平均数

    方差

    小学组

    　　

    85.7

    39.6

    中学组

    85

    　　

    27.8

    （2）考虑平均数与方差，你认为哪个组的团体成绩更好些，并说明理由；

    （3）若在每组的决赛选手中分别选出3人参加总决赛，你认为哪个组获胜的可能性大些？请说明理由．

    查看答案和解析>>

    同步练习册答案