
【题目】对于某个函数,若自变量取实数![]() ,其函数值恰好也等于
,其函数值恰好也等于![]() 时,则称
时,则称![]() 为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差
为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差![]() 称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”
称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”![]() 为0.
为0.
(1)请分别判断函数![]() ,
,![]() ,
,![]() 有没有“等量值”?如果有,直接写出其“等量距离”;
有没有“等量值”?如果有,直接写出其“等量距离”;
(2)已知函数![]() .
.
①若其“等量距离”为0,求![]() 的值;
的值;
②若![]() ,求其“等量距离”
,求其“等量距离”![]() 的取值范围;
的取值范围;
③若“等量距离”![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 没有“等量值”;,函数
没有“等量值”;,函数![]() 有-1和1两个“等量值”,其“等量距离”为2;函数
有-1和1两个“等量值”,其“等量距离”为2;函数![]() 有0和1两个“等量值”,其“等量距离”为1;(2)①
有0和1两个“等量值”,其“等量距离”为1;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
【解析】
(1)根据定义分别求解即可求得答案;
(2)①首先由函数y=2x2-bx=x,求得x(2x-b-1)=0,然后由“等量距离”为0,求得答案;
②由①,利用1≤b≤3,可求得“等量距离”![]() 的取值范围;
的取值范围;
③由②可知,![]() ,解不等式组,即可得到答案.
,解不等式组,即可得到答案.
解:(1)函数![]() 没有“等量值”,
没有“等量值”,
函数![]() 有
有![]() 和1两个“等量值”,其“等量距离”d为2.
和1两个“等量值”,其“等量距离”d为2.
函数![]() 有0和1两个“等量值”,其“等量距离”d为1.
有0和1两个“等量值”,其“等量距离”d为1.
(2)①∵函数![]() 的“等量距离”为零,
的“等量距离”为零,
令![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
②解方程![]() ,
,
得:![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴函数![]() 的“等量距离”
的“等量距离”![]() 的取值范围为:
的取值范围为:![]() .
.
③由②可知,![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ;
;
∴![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
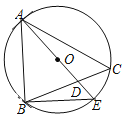
【题目】如图,在△ABC中,∠C=50°,圆O是△ABC的外接圆,AE为圆O的直径,AE与BC相交于点D,若AB=AD.则∠EAC=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
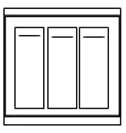
【题目】小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).
(1)若小惠任意闭合一个开关,“客厅灯亮了”是_______事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是_______事件(填“不可能”或“必然”或“随机”);
(2)若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进人积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
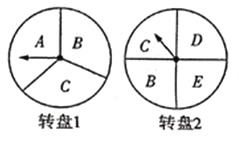
(1)用树状图或列表的方法表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在唐河县文峰广场,耸立着一座古老建筑-文峰塔,传说唐河县城是一个船地, 唐中是船头,文峰塔是船的桅杆,无论唐河水怎么涨,唐河县城这艘船也水涨船高.学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量文峰塔的高度.如图2,刘明在点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() 王华在高台上的点
王华在高台上的点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() ,若高台
,若高台![]() 高为
高为![]() 米,点
米,点![]() 到点
到点![]() 的水平距离EC为
的水平距离EC为![]() 米,且
米,且![]() 三点共线,求该塔
三点共线,求该塔![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,结果保留整数)
,结果保留整数)
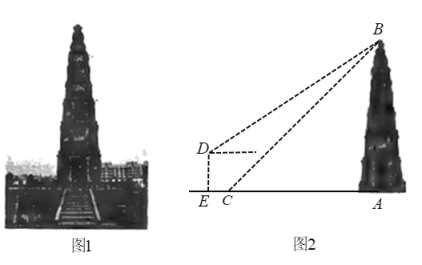
查看答案和解析>>
科目:初中数学 来源: 题型:
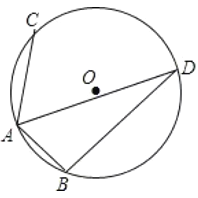
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ,直线
,直线![]() .
.
(1)当![]() 时,求抛物线与
时,求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
(2)直线是否可能经过抛物线的顶点,如果可能,请求出![]() 的值,如果不可能,请说明理由;
的值,如果不可能,请说明理由;
(3)记![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com