
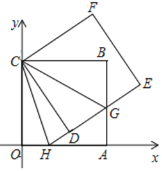
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连结CH、CG.
(1)求证:CG平分∠DCB;
(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;
(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.
【答案】(1)见解析;(2) HG=OH+BG;(3)能成矩形,y![]() .
.
【解析】
(1)根据旋转和正方形的性质可得出CD=CB,∠CDG=∠CBG=90,根据全等直角三角形的判定定理(HL)即可证出Rt△CDG≌Rt△CBG,即∠DCG=∠BCG,由此即可得出CG平分∠DCB;
(2)由(1)的Rt△CDG≌Rt△CBG可得出BG=DG,根据全等直角三角形的判定定理(HL)即可证出Rt△CHO≌Rt△CHD,即OH=HD,再根据线段间的关系即可得出HG=HD+DG=OH+BG;
(3)根据(2)的结论即可找出当G点为AB中点时,四边形AEBD为矩形,再根据正方形的性质以及点B的坐标可得出点G的坐标,设H点的坐标为(x,0),由此可得出HO=x,根据勾股定理即可求出x的值,即可得出点H的坐标,结合点H、G的坐标利用待定系数法即可求出直线DE的解析式.
(1)∵正方形ABCO绕点C旋转得到正方形CDEF,∴CD=CB,∠CDG=∠CBG=90°.在Rt△CDG和Rt△CBG中,∵![]() ,∴Rt△CDG≌Rt△CBG(HL),∴∠DCG=∠BCG,即CG平分∠DCB.
,∴Rt△CDG≌Rt△CBG(HL),∴∠DCG=∠BCG,即CG平分∠DCB.
(2)由(1)证得:Rt△CDG≌Rt△CBG,∴BG=DG.在Rt△CHO和Rt△CHD中,∵![]() ,∴Rt△CHO≌Rt△CHD(HL),∴OH=HD,∴HG=HD+DG=OH+BG.
,∴Rt△CHO≌Rt△CHD(HL),∴OH=HD,∴HG=HD+DG=OH+BG.
(3)假设四边形AEBD可为矩形.
当G点为AB中点时,四边形AEBD为矩形,如图所示.
∵G点为AB中点,∴BG=GA![]() AB,由(2)证得:BG=DG,则BG=GA=DG
AB,由(2)证得:BG=DG,则BG=GA=DG![]() AB
AB![]() DE=GE,又AB=DE,∴四边形AEBD为矩形,∴AG=EG=BG=DG.
DE=GE,又AB=DE,∴四边形AEBD为矩形,∴AG=EG=BG=DG.
∵AG![]() AB=3,∴G点的坐标为(6,3).
AB=3,∴G点的坐标为(6,3).
设H点的坐标为(x,0),则HO=x,∴HD=x,DG=3.
在Rt△HGA中,HG=x+3,GA=3,HA=6﹣x,由勾股定理得:(x+3)2=32+(6﹣x)2,解得:x=2,∴H点的坐标为(2,0).
设直线DE的解析式为:y=kx+b(k≠0),将点H(2,0)、G(6,3)代入y=kx+b中,得:![]() ,解得:
,解得: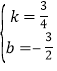 ,∴直线DE的解析式为:y
,∴直线DE的解析式为:y![]() .
.
故四边形AEBD能为矩形,此时直线DE的解析式为:y![]() .
.


科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍,求降价后每枝玫瑰的售价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习全等三角形的判定方法以后,我们知道“已知两边和一角分别相等的两个三角形不一定全等”,但下列两种情形还是成立的.
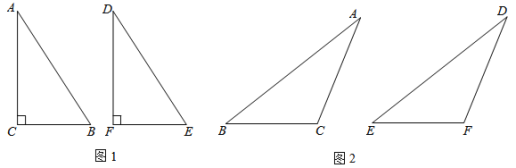
(1)第一情形(如图1)在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据__________,得出△ABC≌△DEF;
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
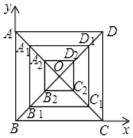
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= ![]() x与y=
x与y= ![]() (k≠0)的图象性质.
(k≠0)的图象性质.
小明根据学习函数的经验,对函数y= ![]() x与y=
x与y= ![]() ,当k>0时的图象性质进行了探究.
,当k>0时的图象性质进行了探究.
下面是小明的探究过程: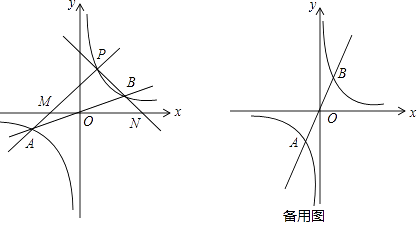
(1)如图所示,设函数y= ![]() x与y=
x与y= ![]() 图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
图象的交点为A,B,已知A点的坐标为(﹣k,﹣1),则B点的坐标为;
(2)若点P为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下,设P(m, ![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则 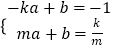 ,
,
解得 ![]()
∴直线PA的解析式为 ![]()
请你把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断△PAB的形状,并用k表示出△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).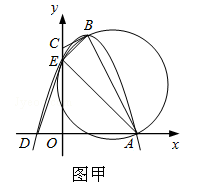
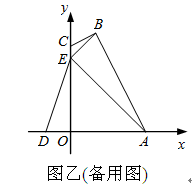
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com