
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠B=30°,AC=6,OA=2,直接写出阴影部分的面积.

【答案】(1)直线DE与⊙O相切;理由见解析;(2)![]() .
.
【解析】
(1)直线DE与⊙O相切,连接OD,由已知条件证明OD⊥DE即可证明DE是⊙O的切线;
(2)连接OE,根据阴影部分的面积=四边形CEDO-扇形DOM的面积计算即可.
(1)直线DE与⊙O相切,理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA,
∵EF是BD的垂直平分线,
∴EB=ED,
∴∠B=∠EDB,
∵∠C=90°,
∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°﹣90°=90°,
即OD⊥DE,
又∵OD为⊙O的半径,
∴直线DE与⊙O相切;
(2)连接OE,
∵∠B=30°,
∴∠A=60°,
∵OD=OA,
∴∠ODA=∠A=60°,
∴AD=AO=DO=2,∠MOD=120°,
∵AC=6,∠B=30°,
∴AB=12,
∴BD=10,
∵EF是BD的垂直平分线,
∴BF=DF=5,
∴EF=![]() ,BE=DE=
,BE=DE=![]() ,
,
∴CE=BC﹣BE=![]() ,
,
∴阴影部分的面积=四边形CEDO﹣扇形DOM的面积=![]() ×
×![]() ×4+
×4+![]() ×
×![]() ×2﹣
×2﹣![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。
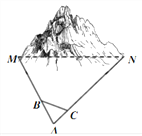
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+
x+![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°.
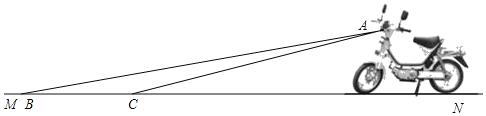
(1)该车大灯照亮地面的宽度BC是1.4m,求大灯A与地面距离约是多少?
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,突然遇到危险情况,立即刹车直到摩托车停止,在这个过程刹车距离是![]() m,请判断(1)中的该车大灯A的地面高度是否能满足最小安全距离的要去,若不能该如何调整A的高度?(参考数据:sin8°≈
m,请判断(1)中的该车大灯A的地面高度是否能满足最小安全距离的要去,若不能该如何调整A的高度?(参考数据:sin8°≈![]() ,tan8°≈
,tan8°≈![]() ,sin10°≈
,sin10°≈![]() ,tan10°≈
,tan10°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点坐标是(﹣2,0),将点A绕原点O顺时针旋转40°,A的对应点是A1,将点A1绕原点O顺时针旋转40°,A1的对应点是A2,将点A2绕原点O顺时针旋转40°,A2的对应点是A3,…,按此规律Ai每次都绕原点O顺时针旋转40°得Ai+1,则A2019的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
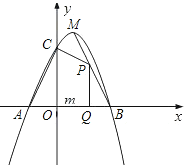
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,求出点
为等腰三角形?如果存在,求出点![]() 的坐标;如果不存在,请说呀理由.
的坐标;如果不存在,请说呀理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:(1)
之间,其部分图象如图所示,则下列结论:(1)![]() :(2)
:(2)![]() ;(3)
;(3)![]() (
(![]() 为任意实数);(4)
为任意实数);(4)![]() ;5)点
;5)点![]()
![]()
![]() 是该抛物线上的点,且
是该抛物线上的点,且![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
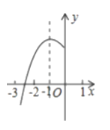
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com