
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:解答题
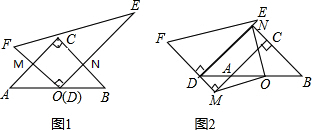
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
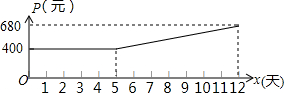 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.| 时间x(天) | 2 | 4 |
| 每天产量y(吨) | 24 | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com