
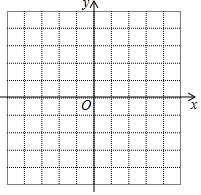
 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),分析 (1)把(0,3)代入y=-x2+(m-1)x+m即可m的值.
(2)根据抛物线的解析式即可画出图象.
(3)求出A、B、D三点的坐标,然后求出直线AD的解析式,过点B作BF⊥x轴于点F,交AD于点E,从而可求出△ABD的面积.
解答 解:(1)把(0,3)代入y=-x2+(m-1)x+m,
∴m=3,
∴抛物线的解析式为:y=-x2+2x+3,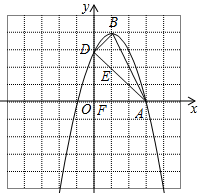
(2)如图所示;
(3)令y=0代入y=-x2+2x+3,
∴0=-x2+2x+3,
∴x=3或x=-1
∴A(3,0)
抛物线的对称轴为x=1,
令x=1代入y=-x2+2x+3,
∴y=4,
∴B(1,4)
令x=0代入y=-x2+2x+3,
∴y=3,
∴D(0,3)
过点B作BF⊥x轴于点F,交AD于点E,
设AD的解析式为y=kx+b,
将点A(3,0)和D(0,3)代入y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$
∴解得:y=-x+3
令x=1代入y=-x+3,
∴y=2,
∴E(1,2),
∴BE=2,
∴S△ABD=S△BDE+S△ABE
=$\frac{1}{2}$BE×OF+$\frac{1}{2}$BE×AF
=$\frac{1}{2}$BE×OA
=$\frac{1}{2}$×2×3
=3
点评 本题考查二次函数的综合问题,解题的关键是求出抛物线的解析式以及抛物线与x轴、y轴的交点,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
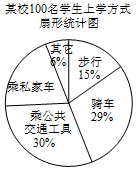 某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):| 方式 | 划记 | 频数 |
| 步行 | 正正正 | 15 |
| 骑车 | 正正正正正 | 29 |
| 乘公共交通工具 | 正正正正正正 | 30 |
| 乘私家车 | ||
| 其它 | ||
| 合计 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
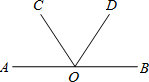 如图,O是直线AB上的一点,OC,OD是两条射线,∠BOD=∠COD,∠BOC=156°,求:
如图,O是直线AB上的一点,OC,OD是两条射线,∠BOD=∠COD,∠BOC=156°,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
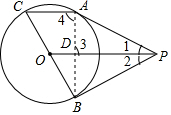 如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.
如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com