练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

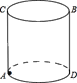
    【题目】如图，圆柱的高为，底面半径为，在圆柱下底面的点处有一只蚂蚁，它想吃到上底面处的食物，已知四边形的边、恰好是上、下底面的直径．为：蚂蚁至少要爬行多少路程才能食到食物？

    【答案】

    【解析】

    求至少要爬多少路程，根据两点之间直线最短，把圆柱体展开，在得到的矩形上连接两点，求出距离即可．

    解：把圆柱体沿着AC直线剪开，得到矩形如下：


    则AB的长度为所求的最短距离，
    根据题意圆柱的高为10cm，底面半径为4cm，
    则可以知道AC=10cm，BC=底面周长，
    ∵底面周长为2πr=2×π×4=8πcm，
    ∴BC=4πcm，
    根据勾股定理得AB2=AC2+BC2，
    即AB2=102+（4π）2，
    ∴AB=cm．
    答：蚂蚁至少要爬行cm路程才能食到食物．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知直线AB∥CD，直线EF与AB，CD分别相交于点E，F．

    （1）如图1，若∠1=60°，求∠2=__________；∠3=__________．

    （2）若点P是平面内的一个动点，连结PE，PF，探索∠EPF，∠PEB，∠PFD三个角之间的关系．

    ①当点P在图2的位置时，可得∠EPF=∠PEB+∠PFD． 理由如下：

    如图2，过点P作MN∥AB，则∠EPM=∠PEB（__________）

    ∵AB∥CD（已知） MN∥AB（作图）

    ∴MN∥CD（__________）

    ∴∠MPF=∠PFD （__________）

    ∴__________+__________=∠PEB+∠PFD（等式的性质）

    即：∠EPF=∠PEB+∠PFD．请补充完整说理过程（填写理由或数学式）

    ②当点P在图3的位置时，此时∠EPF=80°，∠PEB=156°，则∠PFD=__________；

    ③当点P在图4的位置时，写出∠EPF，∠PEB，∠PFD三个角之间的关系并证明（每一步必须注明理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD=BC且AD∥BC，AB=5，AD=3，AE平分∠DAB交BC的延长线于F点，则CF=_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：OB、OC、OM、ON是∠AOD内的射线．

    (1)如图1，若∠AOD=156°，OM平分∠AOB，ON平分∠BOD，∠BOD=96°，则∠MON的度数为　 　．

    (2)如图2，若∠AOD=m°，∠NOC=23°，OM平分∠AOB，ON平分∠BOD，求∠COM的度数(用m的式子表示)；

    (3)如图3，若∠AOD=156°，∠BOC=22°，∠AOB=30°，OM平分∠AOC，ON平分∠BOD，当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时，∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB=CD=8cm，BC=14cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：

    （1）BP= cm（用t的代数式表示）

    （2）当t为何值时，ABPDCP？

    （3）当点P从点B开始运动，同时，点Q从点C出发，以v cm/秒的速度沿CD向点D运动，是否存在这样v的值，使得ABP与PQC全等？若存在，请求出v的值；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积． 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路，完成解答过程．

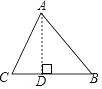
    (1)作AD⊥BC于D，设BD=x，用含x的代数式表示CD，则CD=________；

    (2)请根据勾股定理，利用AD作为“桥梁”建立方程，并求出x的值；

    (3)利用勾股定理求出AD的长，再计算三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，可以理解为，它表示：数轴上表示数的点到原点的距离，这是绝对值的几何意义．进一步地，数轴上的两个点，分别用数表示，那么两点之间的距离为，反过来，式子的几何意义是：数轴上表示数的点和表示数的点之间的距离．利用此结论，回答以下问题：

    （1）数轴上表示数8的点和表示数3的点之间的距离是_________，数轴上表示数的点和表示数的点之间的距离是__________．

    （2）数轴上点用数表示，若，那么的值为_________．

    （3）数轴上点用数表示：

    ①若，那么的值是________．

    ②当时，数的取值范围是________，这样的整数有________个．

    ③有最小值，最小值是___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

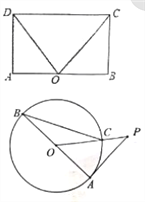
    【题目】（1）如图，在矩形ABCD中.点O在边AB上，∠AOC=∠BOD.求证：AO=OB.

    （2）如图，AB是的直径，PA与相切于点A，OP与相交于点C，连接CB，∠OPA=40°，求∠ABC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(10分)如图①，将两块全等的三角板拼在一起，其中△ABC的边BC在直线l上，AC⊥BC且AC = BC；△EFP的边FP也在直线l上，边EF与边AC重合，EF⊥FP且EF = FP。

    （1）在图①中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；

    （2）将三角板△EFP沿直线l向左平移到图②的位置时，EP交AC于点Q，连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；

    （3）将三角板△EFP沿直线l向左平移到图③的位置时，EP的延长线交AC的延长线于点Q，连接AP、BQ。你认为（2）中猜想的BQ与AP所满足的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由。

    查看答案和解析>>

    同步练习册答案