
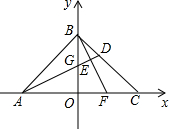
 ��ͼ����ƽ��ֱ������ϵ�У�OA=OB=OC=6����G���߶�OB�ϵ�һ�����㣬����AG���ӳ�BC�ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У�OA=OB=OC=6����G���߶�OB�ϵ�һ�����㣬����AG���ӳ�BC�ڵ�D������ ��1����DH��AC��H����OA=OB=OC=6���Ϳ��Եó���ACB=45�㣬�������ε������ʽ�Ϳ������DH��ֵ���Ϳ������CH��ֵ���Ӷ����D�����ꣻ
��2������OA=OB���ٸ���ֱ�������ε����ʾͿ��Եó���AOG�ա�BOF���Ϳ��Եó�OF=OG���ɡ�AOG�ס�AHD�Ϳ��Եó�OG��ֵ���Ϳ������F�����꣮
��3��������������ͼ��ͼ1����PH��OB��H��PM��OC��M���ɡ�PHB�ա�PMF�Ϳ��Եó����ۣ�ͼ2����PH��OC��H���ɡ�BOF�ա�PHF�Ϳ��Եó����ۣ�ͼ3����PH��OB��H���ɡ�BOF�ա�PHB�Ϳ��Եó����ۣ�
��� �⣺��1����ͼ1��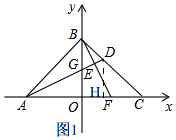
��DH��AC��H��
���AHD=��CHD=90�㣮
��OA=OB=OC=6��
��AC=12��
��S��ABC=$\frac{1}{2}$��6��12=36��
�ߡ�ABD�����Ϊ��ABC�����$\frac{1}{3}$��
���ACD�������ABC�����$\frac{2}{3}$��
��$\frac{2}{3}$��36=$\frac{1}{2}$��12DH��
��DH=4��
��OC=OB��
���BCO=��OBC��
�ߡ�BOC=90�㣬
���BCO=��OBC=45�㣬
���HDC=45�㣬
���HDC=��DCH��
��DH=CH��
��CH=4��
��OH=2��
��D��2��4����
��2����BE��AD��
���BEG=��AEF=90�㣬
�ߡ�AOB=��BOF=90�㣬
���BOF=��AEF=90��
���AFB+��FAG=90�㣬��AFB+��OBF=90�㣬
���FAG=��OBF��
�ڡ�AOG�͡�BOF��$\left\{\begin{array}{l}{��AOG=��BOF}\\{OA=OB}\\{��FAG=��OBF}\end{array}\right.$��
���AOG�ա�BOF��ASA����
��OF=OG��
�ߡ�AOG=��AHD=90�㣬
��OG��DH��
���AOG�ס�AHD��
��$\frac{AO}{AH}=\frac{OG}{DH}$��
��$\frac{6}{8}=\frac{OG}{4}$��
��OG=3��
��OF=3��
��F��3��0��
��3����ͼ2��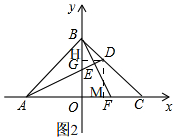 ����BPF=90�㣬PB=PFʱ����PH��OB��H��PM��OC��M
����BPF=90�㣬PB=PFʱ����PH��OB��H��PM��OC��M
���PHB=��PHO=��PMO=��PMC=90��
�ߡ�BOC=90�㣬
���ı���OMPH�Ǿ��Σ�
���HPM=90�㣬
���HPF+��MPF=90�㣮
�ߡ�BPF=90�㣬
���BPH+��HPF=90�㣮
�ߡ�BPH=��FPM��
�ڡ�PHB�͡�PMF��$\left\{\begin{array}{l}{��BPH=��FPM}\\{��BHP=��FMP}\\{BP=FP}\end{array}\right.$��
���PHB�ա�PMF��AAS����
��BH=FM��HP=PM��
�����HPMO��������
��HO=MO=HP=PM��
��CO=OB��
��BO-OH=OC-OM��
��BH=MC��
��FM=MC��
��OF=3��
��FB=3��
��FM=2��
��OM=2
��PM=2��
��P��2��2����
ͼ3�� ����BFP=90�㣬PF=BFʱ����PH��OC��H��
����BFP=90�㣬PF=BFʱ����PH��OC��H��
���OFB+��PFH=90�㣬��PHF=90�㣬
���PFH+��FPH=90�㣬
���OFB=��HPF��
�ߡ�BOF=90�㣬
���BOF=��FHP��
�ڡ�BOF�͡�PHF��$\left\{\begin{array}{l}{��BOF=��FHP}\\{��OFB=��HPF}\\{BF=FP}\end{array}\right.$��
���BOF�ա�PHF��AAS����
��OF=HP��BO=FH��
��HP=3��FH=6��
��OH=9��
��P��9��3����
ͼ4��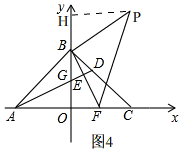 ����FBP=90�㣬PB=BFʱ����PH��OB��H��
����FBP=90�㣬PB=BFʱ����PH��OB��H��
���BHP=90�㣬
���HBP+��HPB=90�㣮
�ߡ�FBP=90�㣬
���HBP+��OBF=90�㣬
���OBF=��HBP��
�ߡ�FOB=90�㣬
���FOB=��BHP��
�ڡ�BOF�͡�PHB�У�$\left\{\begin{array}{l}{��OBF=��HBP}\\{��FOB=��BHP}\\{BF=PB}\end{array}\right.$��
���BOF�ա�PHB��AAS����
��OF=HB��OB=HP��
��HC=3��HP=6��
��HO=9��
��P��6��9����
��P��6��9������9��3������2��2����
���� �������������ۺ��⣬��Ҫ������������ͼ������ʵ����ã�����ֱ�������ε����ʵ����ã������ε������ʽ�����ã�ȫ�������ε��ж������ʵ����ã����ʱ��������ȫ���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��$\frac{1}{2}$a-b�� | B�� | $\frac{1}{2}$a-3b | C�� | 3��a-$\frac{1}{2}$b�� | D�� | ��a-$\frac{1}{2}$��-3b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
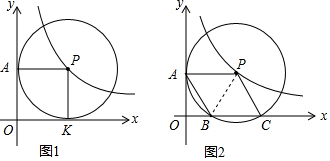
 ��ͼ���ڡ�ABC�У�BD�ǡ�ABC��ƽ���ߣ�DE��BC��BC=7��AE=4����DE�ij���
��ͼ���ڡ�ABC�У�BD�ǡ�ABC��ƽ���ߣ�DE��BC��BC=7��AE=4����DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
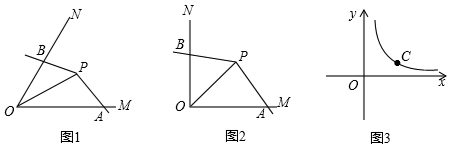 ��ͼ1����PΪ��MON��ƽ������һ�㣬��PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�����APB�Ƶ�P��תʱʼ������OA•OB=OP2�����ǾͰѡ�APB������MON���ǻ۽ǣ�
��ͼ1����PΪ��MON��ƽ������һ�㣬��PΪ����Ľǵ����߷ֱ�������OM��ON����A��B���㣬�����APB�Ƶ�P��תʱʼ������OA•OB=OP2�����ǾͰѡ�APB������MON���ǻ۽ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
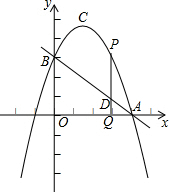 ��ͼ�������߶�������Ϊ��C��2��8������x���ڵ�A ��6��0������y���ڵ�B��
��ͼ�������߶�������Ϊ��C��2��8������x���ڵ�A ��6��0������y���ڵ�B���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com