
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )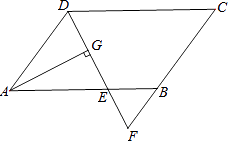
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
【答案】B
【解析】解:∵DE平分∠ADC,
∴∠ADE=∠CDE;
又∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ADE=∠CDF=∠AED,
∴AD=AE=6,
∵AG⊥DE,垂足为G,
∴DE=2DG.
在Rt△ADG中,∵∠AGD=90°,AD=6,AG=4 ![]() ,
,
∴DG= ![]() =2,
=2,
∴DE=2DG=4;
∴S△ADE= ![]() DEAG=
DEAG= ![]() ×4×4
×4×4 ![]() =8
=8 ![]() .
.
∵AE=6,AB=DC=9,
∴BE=AB﹣AE=9﹣6=3,
∴AE:BE=6:3=2:1.
∵AD∥FC,
∴△ADE∽△BFE,
∴S△ADE:S△BFE=(AE:BE)2=4:1,
则S△BEF= ![]() S△ADE=2
S△ADE=2 ![]() .
.
所以答案是:B.
【考点精析】掌握平行四边形的性质和相似三角形的判定与性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
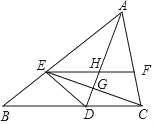
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图: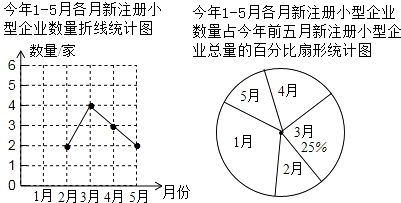
(1)某镇今年1﹣5月新注册小型企业一共有家.请将折线统计图补充完整;
(2)该镇今年4月新注册的小型企业中,只有2家是餐饮企业,现从4月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.

(1)求证:△AEB≌△CDA;
(2)求∠BPQ的度数;
(3)若BQ⊥AD于Q,PQ=6,PE=2,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
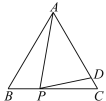
【题目】如图,△ABC为等边三角形,点P为边BC上一点,在AC上取一点D,使AD=AP.
(1)若∠APD=80°,求∠DPC的度数;
(2)若∠APD=α,求∠BAP(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
参考数据:tan58°≈1.60, ![]() ≈1.732,供选用.
≈1.732,供选用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明:两直线平行,同旁内角互补(填空).
已知:如图,l1∥l2,l1,l2都被l3所截.
求证:∠1+∠2=180°.
证明:假设∠1+∠2________180°. ∵l1∥l2,∴∠1________∠3. ∵∠1+∠2 _______180°,∴∠3+∠2≠180°,这和________矛盾,∴假设∠1+∠2__________180°不成立,即∠1+∠2=180°.
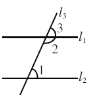
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )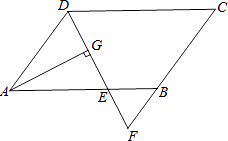
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com