
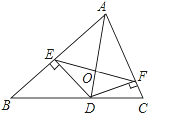
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F. 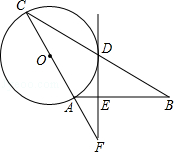
(1)求证:EF⊥AB;
(2)若∠C=30°,EF= ![]() ,求EB的长.
,求EB的长.
【答案】
(1)证明:连接AD、OD
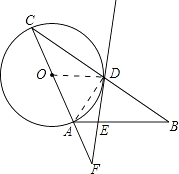 ,
,
∵AC为⊙O的直径,
∴∠ADC=90°,
又∵AB=AC,
∴CD=DB,又CO=AO,
∴OD∥AB,
∵FD是⊙O的切线,
∴OD⊥EF,
∴FE⊥AB
(2)解:∵∠C=30°,
∴∠AOD=60°,
∴∠F=30°,
∴OA=OD= ![]() OF,
OF,
∵∠AEF=90°EF= ![]() ,
,
∴AE= ![]() ,
,
∵OD∥AB,OA=OC=AF,
∴OD=2AE=2 ![]() ,AB=2OD=4
,AB=2OD=4 ![]() ,
,
∴EB=3 ![]()
【解析】(1)连接AD、OD,根据直径所对的圆周角是直角求出∠ADC=90°,根据等腰三角形的性质证明D是BC的中点,得到OD是△ABC的中位线,根据切线的性质证明结论;(2)根据三角形的内角和得到∠AOD=60°,∠F=30°,根据直角三角形的性质得到OA=OD= ![]() OF,求得AE=
OF,求得AE= ![]() 根据平行线等分线段定理得到OD=2AE=2
根据平行线等分线段定理得到OD=2AE=2 ![]() ,AB=2OD=4
,AB=2OD=4 ![]() ,由线段的和差即可得到结论.
,由线段的和差即可得到结论.


科目:初中数学 来源: 题型:
【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供统计图的部分信息如图.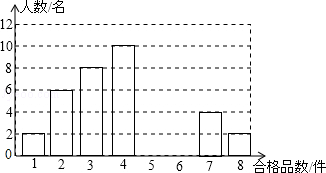
请解答下列问题:
(1)根据统计图,写出这50名工人加工出的合格品数的中位数.
(2)写出这50名工人加工出合格品数的众数的可能取值.
(3)厂方认定,工人在单位时间内加工出的合格品数不低于2件为技能合格,否则,将接受技能再培训,已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
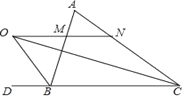
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
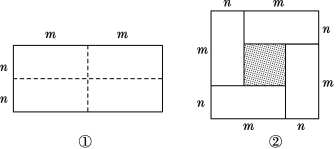
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀把它均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图②中阴影部分的面积.
(3)观察图②你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn.
(4)根据(3)题中的等量关系,解决如下问题:
已知a+b=7,ab=5,求(a-b)2的值.(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC与∠BOD都是直角,∠BOC=65°
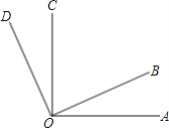
(1)求∠AOD的度数;
(2)∠AOB与∠DOC有何大小关系?
(3)若不知道∠BOC的具体度数,其他条件不变,(2)的关系仍成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
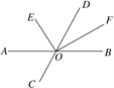
【题目】如图,直线AB、CD交于点O,OE平分∠AOD,OF平分∠BOD.
(1)∠AOC=50°,求∠DOF与∠DOE的度数,并计算∠EOF的度数;
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求其值;若变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).
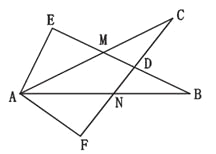
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣2=0.
(1)求证:无论m取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1 , x2 , 且满足x12+x22=﹣3x1x2 , 求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com