
【题目】如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.
(1)画出菱形ABCD,并直接写出n的值及点D的坐标;
(2)已知反比例函数y=![]() 的图象经过点D,ABMN的顶点M在y轴上,N在y=
的图象经过点D,ABMN的顶点M在y轴上,N在y=![]() 的图象上,求点M的坐标;
的图象上,求点M的坐标;
(3)若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.

【答案】(1)n=5,点D坐标为(5,4);(2)M(0,![]() );(3)y=﹣2x+9.
);(3)y=﹣2x+9.
【解析】
(1)由勾股定理和菱形的性质可得AB=BC=CD=AD=5,即可求n的值及点D的坐标;
(2)过点N作NH⊥OA于点H,由平行四边形的性质可得AN=BM,AN∥BM,可得∠BMO=∠NAH,由“AAS”可证△ANH≌△MBO,可得HN=BO=3,MO=AH,即可求点M坐标;
(3)由点A、C、D到某直线l的距离都相等,可得直线l是△ACD的中位线所在直线,由待定系数法可求直线解析式.
解:(1)如图,
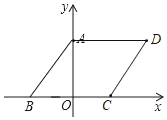
∵点A(0,4)、B(﹣3,0),
∴AO=4,BO=3,
∴AB=![]() =5,
=5,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∵将线段AB沿x轴正方向平移n个单位得到菱形ABCD,
∴n=5,点C坐标为(2,0),点D坐标为(5,4);
(2)∵反比例函数y=![]() 的图象经过点D,
的图象经过点D,
∴k=4×5=20,
∵N在y=![]() 的图象上,
的图象上,
∴设点N(a,![]() ),
),
如图,过点N作NH⊥OA于点H,
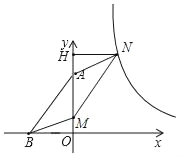
∵四边形ABMN是平行四边形
∴AN=BM,AN∥BM,
∴∠BMA=∠NAM,
∴∠BMO=∠NAH,且AN=BM,∠BOM=∠NHA=90°,
∴△ANH≌△MBO(AAS),
∴HN=BO=3,MO=AH,
∴HN=a=3,HO=![]() ,
,
∴OM=AH=HO﹣AO=![]() ,
,
∴点M(0,![]() );
);
(3)∵点A、C、D到某直线l的距离都相等,
∴直线l是△ACD的中位线所在直线,
如图所示:
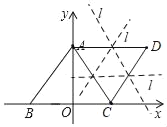
若直线l过线段AC,CD中点,
∴直线l的解析式为:y=2,
若直线l过线段AD,AC中点,即直线l过点(![]() ,4),点(1,2),
,4),点(1,2),
设直线l的解析式为:y=mx+n
∴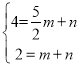 ,
,
解得:m=![]() ,n=
,n=![]() ,
,
∴直线l的解析式为:y=![]() ,
,
若直线l过线段AD,CD中点,即直线l过点(![]() ,4),点(
,4),点(![]() ,2),
,2),
设直线l解析式为:y=kx+b
∴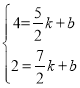 ,
,
解得:k=﹣2,b=9,
∴直线l的解析式为:y=﹣2x+9.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】五一放假期间,甲、乙、丙三位同学到某影城看电影,影城有A,B两部不同电影,甲、乙、丙3人分别从中任选一部观看,每部被选中的可能性相同.
(1)甲同学选择“A部电影”的概率为 ;
(2)用画树状图的方法求甲、乙、丙3人选择同一部电影的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程 7x ![]() (k 13)x k 2 0 ( k 是实数)有两个实数跟 a,b ,且 0 a 1 b 2 ,那么 k 的取值范围是_____.
(k 13)x k 2 0 ( k 是实数)有两个实数跟 a,b ,且 0 a 1 b 2 ,那么 k 的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的4个小球,其中红球3个(记为![]() ,
,![]() ,
,![]() ),黑球1个(记为
),黑球1个(记为![]() ).
).
(1)若先从袋中取出![]() 个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件
个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件![]() ,填空:①若
,填空:①若![]() 为必然事件,则
为必然事件,则![]() 的值为__________;②若
的值为__________;②若![]() 为随机事件,则
为随机事件,则![]() 的取值为_____________;
的取值为_____________;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为![]() 上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,
上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
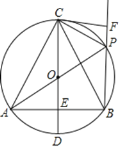
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D′、E′,当直线D′E′经过点A时,线段CD′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承建一段公路路基工程,由乙队先单独施工40天后,甲乙两队共同施工.甲队每天挖土0.425万立方米,乙队工作效率保持不变,设甲、乙两队在此公路施工中的挖土总量![]() (万立方米)与工作时间
(万立方米)与工作时间![]() (天)的函数图象如图所示.
(天)的函数图象如图所示.
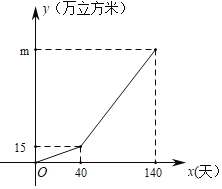
(1)求乙队每天的挖土量;
(2)求此次任务的挖土总量![]() ;
;
(3)求甲、乙两队共同施工时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com