Question

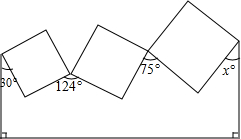
4．如图，三个正方形一些顶点标出了角的度数，则x=41．

Answer 1

分析 首先作出图形，由直角三角形的性质、五边形内角和、四边形内角和，一步步求出x即可．

解答 解：作图如右图所示：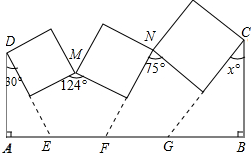
∵∠A=90°，∠ADE=30°，
∴∠DEA=60°，
∴∠DEF=120°，
∵五边形内角和为540°，
∴∠NFE=540°-90°-90°-120°-124°=116°，
∴∠NFG=180°-116°=64°，
∴∠CGF=360°-90°-75°-64°=131°，
∴∠CGB=180°-131°=49°，
∵∠GBC=90°，
∴∠GCB=90°-49°=41°；
即v=41．
故答案为：41．

点评 本题主要考查了直角三角形的性质、五边形内角和、四边形内角和；根据题意作出图形是解答本题的关键．