练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．计算：（$\frac{3}{2}$$\sqrt{1\frac{2}{3}}$+$\sqrt{1\frac{1}{4}}$）2．

    分析 利用完全平方公式进行计算．

    解答 解：原式=$\frac{9}{4}×\frac{5}{3}+2×\frac{3}{2}\sqrt{\frac{5}{3}}×\sqrt{\frac{5}{4}}+\frac{5}{4}$
    =$\frac{15}{4}+3\sqrt{\frac{25}{12}}+\frac{5}{4}$
    =$5+\frac{{5\sqrt{3}}}{2}$．

    点评 本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

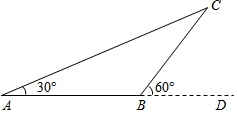    20．如图，小丽想知道自家门前小河的宽度，于是她测出如下数据：在河岸选取A点，A点对岸选取参照点C，测得∠A=30°；她沿河岸向前走了30米选取点B，并测得∠CBD=60°．根据数据能否测得小河宽度？若能请算出小河宽度，若不能请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．长、宽分别为a、b长长方形，它的周长为16，面积为10，则a2b+ab2的值为80．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，过点B作BK⊥AC，垂足为K，过D作DH∥KB，DH分别与AC，AB，⊙O及CB的延长线相交于点E，F，G，H，且F是EG的中点．
    （1）求证：点D在⊙O上；
    （2）求证：F是AB的中点；
    （3）若DE=4，求⊙O的半径和△BFH的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知，OB∥AC，∠B=∠A=110°，试回答下列问题：

    （1）如图①，说明BC∥OA的理由．
    （2）如图②，若点E、F在线段BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF．则∠EOC等于35度；（在横线上填上答案即可）．
    （3）在（2）的条件下，若左右平行移动AC，如图③，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值．
    （4）在（2）的条件下，如果平行移动AC的过程中，如图③，若使∠OEB=∠OCA，此时∠OCA等于52.5度．（在横线上填上答案即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．【问题提出】如图1．△ABC是等边三角形，点D在线段AB上．点E在直线BC上．且∠DEC=∠DCE．求证：BE=AD；
    【类比学习】如图2．将条件“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变．判断线段AB、BE、BD之间的数量关系，并说明理由．
    【扩展探究】如图3．△ABC是等腰三角形，AB=AC，∠BAC=120°，点D在线段AB的反向延长线上，点E在直线BC上，且∠DEC=∠DCE，【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立？若成立，请说明理由；若不成立，请直接写出线段AB，BE，BD之间的数量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

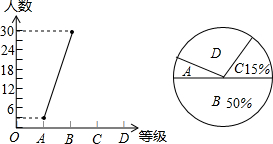    2．为迎接常熟市文明城市创建工作，某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动，成绩分为A、B、C、D四个等级，并将收集的数据绘制了两幅不完整的统计图．请你根据图中所给出的信息，解答下列各题：
    （1）求八年级一班共有多少人；
    （2）补全折线统计图；
    （3）在扇形统计图中等极为“D”的部分所占圆心角的度数为108°；
    （4）若等级A为优秀，求该班的优秀率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在△ABC中，AB=BC，BD⊥AC于点D．
    （1）如图1，当∠ABC=90°时，若CE平分∠ACB，交AB于点E，交BD于点F．
    ①求证：△BEF是等腰三角形；
    ②求证：BD=$\frac{1}{2}$（BC+BF）；
    （2）点E在AB边上，连接CE．若BD=$\frac{1}{2}$（BC+BE），在图2中补全图形，判断∠ACE与∠ABC之间的数量关系，写出你的结论，并写出求解∠ACE与∠ABC关系的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．先化简，再求值：$\frac{x-2}{{x}^{2}-1}$•$\frac{x+1}{{x}^{2}-4x+4}$+$\frac{1}{x-1}$，从-1，0，1三个数中选一个合适的，代入求值．

    查看答案和解析>>

    同步练习册答案