
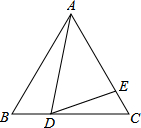
 如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$.
如图,在边长为9的正三角形ABC中,BD=4,∠ADE=60°,则CE的长为$\frac{20}{9}$. 分析 由等边三角形的性质可得到∠B=∠C,再根据三角形外角的性质可求得∠EDC=∠BAD,可证得△ABD∽△DCE,由相似三角形的对应边成比例可求得CE.
解答 解:∵△ABC为等边三角形,
∴AB=BC=9,∠B=∠C=60°,
又∵∠ADE=60°,
∴∠ADE+∠EDC=∠B+∠BAD,
∴∠BAD=∠EDC,
∴△ABD∽△DCE,
∴$\frac{BD}{CE}$=$\frac{AB}{CD}$,
∵BD=4,
∴CD=5,
∴$\frac{4}{CE}$=$\frac{9}{5}$,
∴CE=$\frac{20}{9}$,
故答案为:$\frac{20}{9}$.
点评 本题主要考查相似三角形的判定和性质,由条件得到∠BAD=∠EDC是解题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
 把表示下列各数的点画在数轴上,再按从小到大的顺序,用“<”号把这些数连接起来:2$\frac{1}{2}$,-1.5,0,-(+3),-4.
把表示下列各数的点画在数轴上,再按从小到大的顺序,用“<”号把这些数连接起来:2$\frac{1}{2}$,-1.5,0,-(+3),-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
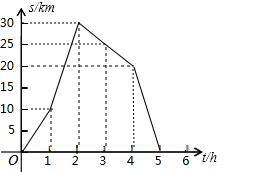 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com