
如图,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
(1)求a的值;
(2)求A,B两点的坐标;
(3)以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D´是否在该抛物线上?请说明理由.

答案:解:(1)抛物线y=x2﹣x+a=(x2﹣2x)+a=(x﹣1)2﹣+a,
∴抛物线顶点坐标为:(1,﹣ +a)
∵抛物线y=x2﹣x+a其顶点在直线y=﹣2x上
则将顶点坐标代入y=﹣2x得
﹣+a=﹣2,∴a=﹣; (2分)
(2)由(1)写出抛物线解析式为:y=x2﹣x﹣
∵抛物线y=x2﹣x﹣与x轴交于点A、B,
∴0=x2﹣x﹣,整理得:x2﹣2x﹣3=0,
解得:x=﹣1或3,
∴A(﹣1,0),B(3,0); (5分)
(3)作出平行四边形ACBD,作DE⊥AB,

∵二次函数解析式为:y=x2﹣x﹣
∴图象与y轴交点坐标为:(0,﹣),∴CO=,DE= (7分)
∵∠CAO=∠DBE,∠DEB=∠AOC ∴△AOC≌△BDE
∴AO=BE=1, OE=OB-BE=2
∴D点的坐标为:(2,), (9分)
则点D关于x轴的对称点D′坐标为:(2,﹣),
代入解析式y=x2﹣x﹣,左边=﹣,右边=×4﹣2﹣=﹣,
∴D′点在函数图象上.(10分)


科目:初中数学 来源: 题型:
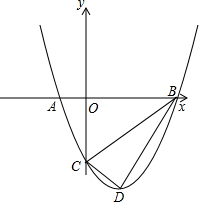 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
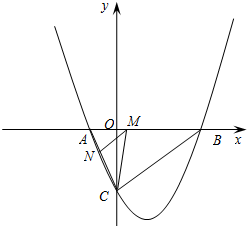 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.查看答案和解析>>
科目:初中数学 来源: 题型:
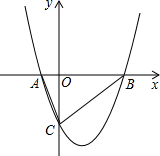 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com