练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2011•陕西）下列四个点，在正比例函数的图象上的点是（　　）
    A．（2，5）B．（5，2）
    C．（2，﹣5）D．（5，﹣2
    D
    由，得=﹣；
    A、∵=，故本选项错误；
    B、∵=，故本选项错误；
    C、∵=﹣，故本选项错误；
    D、∵=﹣，故本选项正确；
    故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    （本题满分12分）我们设想用电脑模拟台球游戏，为简单起见，约定：①每个球袋视为一个点，如果不遇到障碍，各球均沿直线前进；②A球击B球，意味着B球在A球前进的路线上，且B球被撞击后沿A球原来的方向前进；③球撞击桌边后的反弹角度等于入射角度，（如图中∠β=∠a）如图所示，设桌边只剩下白球，A，6号球B。
    （1）希望A球撞击桌边上C点后反弹，再击中B球，请给出一个算法，告知电脑怎样找到点C，并求出C点的坐标。
    （2）设桌边RQ上有一球袋S（100，120），判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中，（假定6号球被撞后速度足够大）。
    （3）若用白球A直接击打6号球B，使6号球B撞击桌边OP上的D点后反弹，问6号球B从D点反弹后能否直接进入球袋Q中？（假定6号球被撞后速度足够大）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （2011•黑河）已知直线y=x+4与x轴、y轴分别交于A、B两点，∠ABC=60°，BC与x轴交于点C．
    （1）试确定直线BC的解析式．
    （2）若动点P从A点出发沿AC向点C运动（不与A、C重合），同时动点Q从C点出发沿CBA向点A运动（不与C、A重合），动点P的运动速度是每秒1个单位长度，动点Q的运动速度是每秒2个单位长度．设△APQ的面积为S，P点的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围．
    （3）在（2）的条件下，当△APQ的面积最大时，y轴上有一点M，平面内是否存在一点N，使以A、Q、M、N为顶点的四边形为菱形？若存在，请直接写出N点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

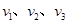    小可骑车上学，路上要经过平路、下坡、上坡和平路（如图），若小可上坡、平路、下坡的速度分别为：且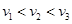，则小可骑车上学时，离家的距离s与所用时间t的函数关系图像大致是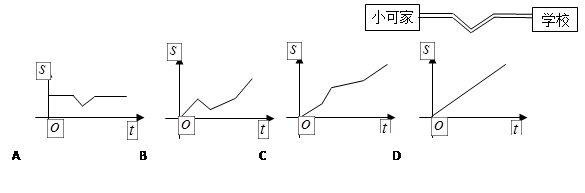

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    一次函数的图像经过点（1，0），且y随x的增大而减小，这个一次函数的关
    系式可以是  ▲ ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （2011•攀枝花）某经营世界著名品牌的总公司，在我市有甲、乙两家分公司，这两家公司都销售香水和护肤品．总公司现香水70瓶，护肤品30瓶，分配给甲、乙两家分公司，其中40瓶给甲公司，60瓶给乙公司，且都能卖完，两公司的利润（元）如下表．
    （1）假设总公司分配给甲公司x瓶香水，求：甲、乙两家公司的总利润W与x之间的函数关系式；
    （2）在（1）的条件下，甲公司的利润会不会比乙公司的利润高？并说明理由；
    （3）若总公司要求总利润不低于17370元，请问有多少种不同的分配方案，并将各种方案设计出来．
     
    		每瓶香水利润
    		每瓶护肤品利润
    甲公司
    		180
    		200
    乙公司
    		160
    		150

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （11·兵团维吾尔）（10分）某商场推销一种书包，进价为30元，在试销中发现
    这种书包每天的销售量P（个）与每个书包销售价x（元）满足一次函数关系式．当定价为
    35元时，每天销售30个；定价为37元时，每天销售26个．问：如果要保证商场每天销售
    这种书包获利200元，求书包的销售单价应定为多少元？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    （11·贺州）写出一个正比例函数，使其图象经过第二、四象限：_  ▲  ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （2011•北京）如图，在平面直角坐标系xOy中，我把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C（注：不含AB线段）．已知A（﹣1，0），B（1，0），AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．
    （1）求两条射线AE，BF所在直线的距离；
    （2）当一次函数y=x+b的图象与图形C恰好只有一个公共点时，写出b的取值范围；
    当一次函数y=x+b的图象与图形C恰好只有两个公共点时，写出b的取值范围；
    （3）已知?AMPQ（四个顶点A，M，P，Q按顺时针方向排列）的各顶点都在图形C上，且不都在两条射线上，求点M的横坐标x的取值范围．

    查看答案和解析>>

    同步练习册答案