
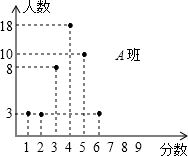
 ��2012•�����ض�ģ������A��B�����༶��ÿ���༶����45��ѧ���μ�һ�β��飬ÿ���μ��߿ɻ��0��1��2��3��4��5��6��7��8��9���⼸�ֲ�ͬ��ֵ�е�һ�֣����Խ��A��ijɼ�����ͼ��ʾ��B��ijɼ������ʾ��
��2012•�����ض�ģ������A��B�����༶��ÿ���༶����45��ѧ���μ�һ�β��飬ÿ���μ��߿ɻ��0��1��2��3��4��5��6��7��8��9���⼸�ֲ�ͬ��ֵ�е�һ�֣����Խ��A��ijɼ�����ͼ��ʾ��B��ijɼ������ʾ��| ���� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| ���� | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
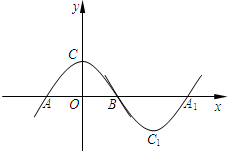 ��2012•�����ض�ģ����ͼ��������m��y=ax2+b��a��0��b��0����x���ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C����������m�Ƶ�B��ת180�㣬�õ��µ�������n�����Ķ���ΪC1����x�����һ������ΪA1�����ı���AC1A1CΪ���Σ���a��bӦ����Ĺ�ϵʽΪ��������
��2012•�����ض�ģ����ͼ��������m��y=ax2+b��a��0��b��0����x���ڵ�A��B����A�ڵ�B����ࣩ����y�ύ�ڵ�C����������m�Ƶ�B��ת180�㣬�õ��µ�������n�����Ķ���ΪC1����x�����һ������ΪA1�����ı���AC1A1CΪ���Σ���a��bӦ����Ĺ�ϵʽΪ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 16 |
| 3 |
| 16 |
| 3 |
| 88 |
| 9 |
| 88 |
| 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 2 |
| k |
| x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com