
ЁОЬтФПЁПЁАЬЋдЪаХњЗЂЪаГЁЁБгыЁАЮїАВЪаХњЗЂЪаГЁЁБжЎМфЕФЩЬвЕЭљРДЦЕЗБЃЌ ШчЭМЃЌЁАЬЋдЪаХњЗЂЪаГЁЁБЁАЮїАВЪаХњЗЂЪаГЁЁБгыЁАГЄЭОЦћГЕеОЁБдкЭЌвЛЯпТЗЩЯЃЌУПЬьжаЮч12:00вЛСОПЭГЕгЩЁАЬЋдЪаХњЗЂЪаГЁЁБЪЛЭљЁАГЄЭОЦћГЕеОЁБЃЌвЛСОЛѕГЕгЩЁАЮїАВЪаХњЗЂЪаГЁЁБЪЛЭљЁАЬЋдЪаХњЗЂЪаГЁЁБЃЌМйЩшСНГЕЭЌЪБГіЗЂЃЌдШЫйааЪЛЃЌЭМ2ЗжБ№ЪЧПЭГЕЁЂЛѕГЕЕНЁАГЄЭОЦћГЕеОЁБЕФОрРы![]() гыааЪЛЪБМф
гыааЪЛЪБМф![]() жЎМфЕФКЏЪ§ЭМЯёЃЎ
жЎМфЕФКЏЪ§ЭМЯёЃЎ
ЧыФуИљОнЭМЯѓаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉгЩЭМ 2 ПЩжЊПЭГЕЕФЫйЖШЮЊ km/hЃЌЛѕГЕЕФЫйЖШЮЊ km/hЃЛ
ЃЈ2ЃЉИљОнЭМ 2 жБНгаДГіжБЯп BC ЕФКЏЪ§ЙиЯЕЪНЮЊ ЃЌжБЯп AD ЕФКЏЪ§ЙиЯЕЪНЮЊ ЃЛ
ЃЈ3ЃЉЧѓЕуBЕФзјБъЃЌВЂНтЪЭЕуBЕФЪЕМЪвтвхЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЃЌ30ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉЕу
ЃЛЃЈ3ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ДњБэЕФЪЕМЪвтвхЪЧДЫЪБПЭГЕКЭЛѕГЕЯргіЃЎ
ДњБэЕФЪЕМЪвтвхЪЧДЫЪБПЭГЕКЭЛѕГЕЯргіЃЎ
ЁОНтЮіЁП
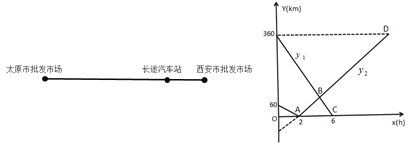
ЃЈ1ЃЉгЩЭМЯѓПЩжЊПЭГЕ6аЁЪБааЪЛЕФТЗГЬЪЧ360ЧЇУзЃЌЛѕГЕ2аЁЪБааЪЛЕФТЗГЬЮЊ60ЧЇУзЃЌДгЖјПЩвдЧѓЕУПЭГЕКЭЛѕГЕЕФЫйЖШЃЛ
ЃЈ2ЃЉЯШЧѓГіЕуDЕФКсзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЃЌРћгУЕуЃЈ0ЃЌ360ЃЉКЭЃЈ6ЃЌ0ЃЉЧѓГіжБЯпBCЕФНтЮіЪНЃЌРћгУЕуAКЭЕуDзјБъЧѓГіжБЯпADЕФНтЮіЪНЃЌМДПЩЕУЕНД№АИ.
ЃЈ3ЃЉАбжБЯпBCКЭжБЯпADСЊКЯЃЌзщГЩЗНГЬзщЃЌМДПЩЧѓГіЕуBЕФзјБъЃЌШЛКѓЕУЕНД№АИ.
НтЃК![]() гЩЭМЯѓПЩЕУЃЌ
гЩЭМЯѓПЩЕУЃЌ
ПЭГЕЕФЫйЖШЪЧЃК360ЁТ6=60 km/hЃЌ
ЛѕГЕЕФЫйЖШЪЧЃК![]() km/hЃЌ
km/hЃЌ
ЙЪД№АИЮЊЃК60ЃЛ30.
![]() ИљОнЬтвтЃЌЛѕГЕааЪЛШЋГЬЫљгУЕФЪБМфЮЊЃК
ИљОнЬтвтЃЌЛѕГЕааЪЛШЋГЬЫљгУЕФЪБМфЮЊЃК![]() аЁЪБЃЛ
аЁЪБЃЛ
ЁрЕуDЕФзјБъЮЊЃЈ14ЃЌ360ЃЉЃЛ
ЩшжБЯпBCЮЊ![]() ЃЌАбЕуЃЈ0ЃЌ360ЃЉКЭЃЈ6ЃЌ0ЃЉДњШыЃЌЕУ
ЃЌАбЕуЃЈ0ЃЌ360ЃЉКЭЃЈ6ЃЌ0ЃЉДњШыЃЌЕУ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпBCЮЊЃК![]() ЃЛ
ЃЛ
ЩшжБЯпADЮЊ![]() ЃЌАбЕуAЃЈ2ЃЌ0ЃЉКЭЕуDЃЈ14ЃЌ360ЃЉДњШыЃЌЕУ
ЃЌАбЕуAЃЈ2ЃЌ0ЃЉКЭЕуDЃЈ14ЃЌ360ЃЉДњШыЃЌЕУ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпADЮЊЃК![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
![]() гЩ
гЩ![]() жЊЃЌПЭГЕгЩЁАЬЋдЪаХњЗЂЪаГЁЁБЕНЁАГЄЭОЦћГЕеОЁБЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊЃК
жЊЃЌПЭГЕгЩЁАЬЋдЪаХњЗЂЪаГЁЁБЕНЁАГЄЭОЦћГЕеОЁБЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊЃК
![]()
ЛѕГЕгЩЁАГЄЭОЦћГЕеОЁБЕНЁАЬЋдЪаХњЗЂЪаГЁЁБЖдгІЕФКЏЪ§ЙиЯЕЪНЮЊЃК![]() ЃЌ
ЃЌ
![]()
НтЕУЃК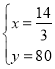 ЃЛ
ЃЛ
![]() Еу
Еу![]() ЕФзјБъЮЊЃК
ЕФзјБъЮЊЃК![]() ЃЛ
ЃЛ
ЁрЕу![]() ДњБэЕФЪЕМЪвтвхЪЧДЫЪБПЭГЕКЭЛѕГЕЯргіЃЎ
ДњБэЕФЪЕМЪвтвхЪЧДЫЪБПЭГЕКЭЛѕГЕЯргіЃЎ


 ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ
ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() КЭ
КЭ![]() ЖМЪЧЕШБпШ§НЧаЮЃЌ
ЖМЪЧЕШБпШ§НЧаЮЃЌ![]() КЭ
КЭ![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЯТСаНсТлжаЃЌе§ШЗЕФга________ИіЃЎ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЦНЗж
ЦНЗж![]() ЃЛЂм
ЃЛЂм![]() ЦНЗж
ЦНЗж![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЧыбЁдёЃЈ2ЃЉжаШЮвЛе§ШЗНсТлНјаажЄУїЃЎФубЁЕФађКХЪЧ _________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌзЊХЬЕФАзЩЋЩШаЮКЭКкЩЋЩШаЮЕФдВаФНЧЗжБ№ЮЊ240ЁуКЭ120Ёу.ШУзЊХЬздгЩзЊЖЏ2ДЮЃЌдђжИеывЛДЮТфдкАзЩЋЧјгђЃЌСэвЛДЮТфдкКкЩЋЧјгђЕФИХТЪЪЧ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
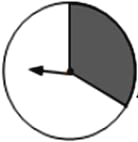
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌ![]() =
=![]() ЃЌЕуDдкБпBCЩЯЃЌAEЁЮBCЃЌAE=BDЃЎ
ЃЌЕуDдкБпBCЩЯЃЌAEЁЮBCЃЌAE=BDЃЎ
ЃЈ1ЃЉЧѓжЄЃКAD=CEЃЛ
ЃЈ2ЃЉШчЙћЕуGдкЯпЖЮDCЩЯЃЈВЛгыЕуDжиКЯЃЉЃЌЧвAG=ADЃЌЧѓжЄЃКЫФБпаЮAGCEЪЧЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжгаМзЃЌввСНИіЙЄГЬЖгЗжБ№ЭЌЪБПЊЭкСНЬѕ 600 m ГЄЕФЫэЕРЃЌЫљЭкЫьЕРГЄЖШ yЃЈmЃЉгыЭкОђЪБМфxЃЈЬьЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎдђЯТСаЫЕЗЈжаЃЌДэЮѓЕФЪЧЃЈ ЃЉ
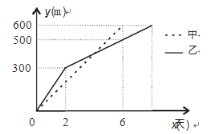
A.МзЖгУПЬьЭк 100 m
B.ввЖгПЊЭкСНЬьКѓЃЌУПЬьЭк50Уз
C.МзЖгБШввЖгЬсЧА2ЬьЭъГЩШЮЮё
D.ЕБ![]() ЪБЃЌМзЁЂввСНЖгЫљЭкЙмЕРГЄЖШЯрЭЌ
ЪБЃЌМзЁЂввСНЖгЫљЭкЙмЕРГЄЖШЯрЭЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггыЁбOЃЌABЪЧжБОЖЃЌЁбOЕФЧаЯпPCНЛBAЕФбгГЄЯпгкЕуPЃЌOFЁЮBCНЛACгкACЕуEЃЌНЛPCгкЕуFЃЌСЌНгAFЃЎ
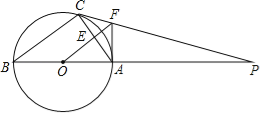
ЃЈ1ЃЉХаЖЯAFгыЁбOЕФЮЛжУЙиЯЕВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ4ЃЌAF=3ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЕуEЁЂFЗжБ№дкБпABКЭCDЩЯЃЌЯТСаЬѕМўВЛФмХаЖЈЫФБпаЮDEBFвЛЖЈЪЧЦНааЫФБпаЮЕФЪЧЃЈ ЃЉ

A.AEЃНCFB.DEЃНBFC.ЁЯADEЃНЁЯCBFD.ЁЯAEDЃНЁЯCFB
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
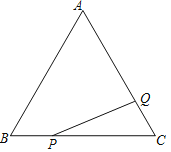
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШБпЁїABCЕФБпГЄЮЊ4ЃЌЕуPЃЌQЗжБ№ЪЧБпBCЃЌACЩЯвЛЕуЃЌPBЃН1ЃЌдђPAЃН_____ЃЌШєBQЃНAPЃЌдђAQЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋcЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌгаЯТСа5ИіНсТлЃК Ђй c=0ЃЛЂкИУХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=Љ1ЃЛЂлЕБx=1ЪБЃЌy=2aЃЛЂмam![]() +bm+aЃО0ЃЈmЁйЉ1ЃЉЃЛЂнЩшAЃЈ100ЃЌyЃЉЃЌBЃЈЉ100ЃЌy
+bm+aЃО0ЃЈmЁйЉ1ЃЉЃЛЂнЩшAЃЈ100ЃЌyЃЉЃЌBЃЈЉ100ЃЌy![]() ЃЉдкИУХзЮяЯпЩЯЃЌдђyЃОy
ЃЉдкИУХзЮяЯпЩЯЃЌдђyЃОy![]() ЃЎЦфжае§ШЗЕФНсТлга___________ ЃЎЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЃЎЦфжае§ШЗЕФНсТлга___________ ЃЎЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com