
【题目】
(1)计算:( ![]() ﹣2)0﹣(﹣1)2017+
﹣2)0﹣(﹣1)2017+ ![]() ﹣sin45°;
﹣sin45°;
(2)化简:( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() .
.
【答案】
(1)解:原式=1+1+ ![]() ﹣
﹣ ![]() =2
=2
(2)解:原式=[ ![]() ﹣
﹣ ![]() ](x﹣1)=﹣
](x﹣1)=﹣ ![]() (x﹣1)=﹣
(x﹣1)=﹣ ![]()
【解析】(1)先根据零指数幂的性质、有理数的乘方法则、二次根式化简法则以及特殊角的三角函数值化简,然后再进行实数运算;
(2)先算括号内的减法(通分),把除法转化成乘法约分即可.
【考点精析】掌握分式的混合运算和零指数幂法则是解答本题的根本,需要知道运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】近年来,越来越多人关注环保和健康问题,为了调查学生对雾霾天气知识的了解程度,某校学生会在全校学生中随机抽取部分同学进行了一次调查,调查结果共分为四个等级组:A.非常了解;B.比较了解;C.基本了解;D.不了解.学生会根据调查统计结果,绘制了不完整的两种统计图.请结合统计图,回答下列问题
(1)本次参与调查的学生总人数为 人;
(2)请在图1中补全条形统计图;
(3)在图2所示的扇形统计图中,请求出“B.比较了解”部分扇形所对应的圆心角是多少度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在市区内,我市乘坐出租车的价格![]() (元)与路程
(元)与路程![]() (km)的函数关系图象如图所示.
(km)的函数关系图象如图所示.

(1)请你根据图象写出两条信息;
(2)小明从学校出发乘坐出租车回家用了13元,求学校离小明家的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).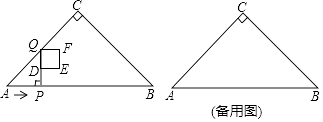
(1)当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(b,-2a).且![]() +|b-l|=0.CD∥AB,AD∥BC
+|b-l|=0.CD∥AB,AD∥BC
(1)直接写出B、C、D各点的坐标:B 、C 、D ;
(2)如图1,P(3,10),点E,M在四边形ABCD的边上,且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形,请直接写出点E的坐标,并对其中一种情况计算说明;
(3)如图2,F为y轴正半轴上一动点,过F的直线j∥x轴,BH平分∠FBA交直线j于点H.G为BF上的点,且∠HGF=∠FAB,F在运动中FG的长度是否发生变化?若变化,求出变化范围;若不变,求出定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com