

 ,
,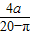 )2+
)2+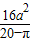 ,
, <
<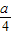 ,
,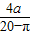 时,S有最大值,
时,S有最大值,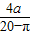 ≠
≠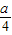 ,
,

科目:初中数学 来源: 题型:
| 3 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏泰州永安初级中学九年级上学期期中考试数学试卷(解析版) 题型:解答题
问题探究:
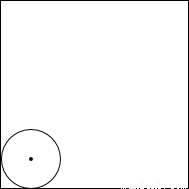
(1)请在图①中作出两条直线,使它们将圆面四等分;

(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M)使它们将正方形ABCD的面积四等分,并说明理由.

问题解决:
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=a,CD=b,且b>a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?如若存在,求出BQ的长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(陕西卷)数学(解析版) 题型:解答题
问题探究
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB= ,CD=
,CD= ,且
,且 ,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源:2013年陕西省中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com