
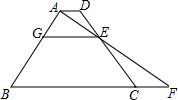
 如图,在梯形ABCD中,AD∥BC,AB=CD,过A作AE⊥AB交CD于E,交BC延长线于F,点E恰好是CD的一个三等分点(CE>ED),过E作BC的平行线与AB交于点G.若EG=3,CF=2,则梯形ABCD的面积为12$\sqrt{2}$.
如图,在梯形ABCD中,AD∥BC,AB=CD,过A作AE⊥AB交CD于E,交BC延长线于F,点E恰好是CD的一个三等分点(CE>ED),过E作BC的平行线与AB交于点G.若EG=3,CF=2,则梯形ABCD的面积为12$\sqrt{2}$. 分析 取GB的中点H,HK∥BC,作AM⊥BC于M,DN⊥BC于N,根据平行线的性质求出AD的长,根据梯形中位线定理求出HK、BC的长,根据勾股定理求出AM的长,根据梯形大面积公式计算得到答案.
解答 解:取GB的中点H,作 HK∥BC,作AM⊥BC于M,DN⊥BC于N,
HK∥BC,作AM⊥BC于M,DN⊥BC于N,
∵AD∥BC,点E恰好是CD的一个三等分点,CF=2,
∴$\frac{AD}{CF}$=$\frac{DE}{EC}$=$\frac{1}{2}$,
∴AD=1,
由梯形的中位线定理可知,HK=5,BC=7,
BM=(BC-AD)÷2=3,
∵AE⊥AB,AM⊥BC,∠AGE=∠ABM,
∴△AGE∽△MBA,
∴$\frac{AG}{BM}$=$\frac{GE}{AB}$,即$\frac{\frac{1}{3}AB}{3}$=$\frac{3}{AB}$,
解得,AB=3$\sqrt{3}$,
∴AM=3$\sqrt{2}$,
∴梯形ABCD的面积为$\frac{1}{2}$×(1+7)×3$\sqrt{2}$=12$\sqrt{2}$,
故答案为:12$\sqrt{2}$.
点评 本题考查的是等腰梯形的性质和梯形的中位线定理,掌握梯形的中位线平行于两底且等于两底和的一半是解题的关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 水位变化(米) | 0.12 | -0.02 | -0.13 | -0.20 | -0.08 | -0.02 | 0.32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)
已知反比例函数y1=$\frac{k}{x}$和一次函数y=x+b的图象都经过(2,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
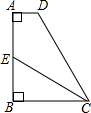 如图,在四边形ABCD中,AD∥BC,AB⊥AD,CE平分∠DCB交AB于E,点E是AB的中点.
如图,在四边形ABCD中,AD∥BC,AB⊥AD,CE平分∠DCB交AB于E,点E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com