练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．解方程组：$\left\{\begin{array}{l}{3（x+y）+2（x-y）=11}\\{6（x+y）-5（x-y）=13}\end{array}\right.$．

    分析 方程组利用加减消元法求出解即可．

    解答 解：方程组整理得：$\left\{\begin{array}{l}{5x+y=11①}\\{x+11y=13②}\end{array}\right.$，
    ②×5-①得：54y=54，即y=1，
    把y=1代入②得：x=2，
    则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$．

    点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法为：加减消元法与代入消元法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．只用下列正多边形地砖中的一种，不能镶嵌的是（　　）
    A．正三角形B．正四边形C．正五边形D．正六边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

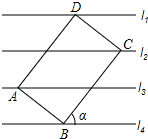    7．已知直线l1∥l2∥l3∥l4，相邻的两条平行直线间的距离均为h，矩形ABCD的四个顶点分别在这四条直线上，放置方式如图所示，AB=6，BC=8，则tanα的值等于（　　）
    A．2：3B．3：4C．4：3D．3：2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．【问题情境】如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．
    【结论运用】如图2，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；
    【迁移拓展】图3是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，
    ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE=DE•BC，AB=8，AD=3，BD=7；M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解方程组：
    （1）$\left\{\begin{array}{l}{x+y=5}\\{x+z=12}\\{y=2z}\end{array}\right.$        
    （2）$\left\{\begin{array}{l}{x+y+z=26}\\{x-y=1}\\{2x+z-y=18}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知方程组$\left\{\begin{array}{l}{ax+5y=15①}\\{4x-by=-2②}\end{array}\right.$由于甲看错了方程①中的a，得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$，乙看错了方程②中的b，得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$，试求出a，b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知关于x、y的方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-2y=m}\end{array}\right.$．
    （1）求这个方程组的解；
    （2）当m取何值时，这个方程组的解满足x-y＞3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解方程组：$\left\{\begin{array}{l}{x-y-z=5}\\{y-z-x=1}\\{z-x-y=-15}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

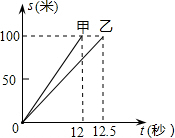    6．甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示．下列关于此次赛跑说法正确的是（　　）
    A．乙比甲跑的路程多B．这是一次100米赛跑
    C．甲乙同时到达终点D．甲的速度为8m/s

    查看答案和解析>>

    同步练习册答案