
分析 (1)根据式子规律可得2n-2n-1=2n-1,然后利用提公因式2n-1可以证明这个等式成立;
(2)设题中的表达式为a,再根据同底数幂的乘法得出2a的表达式,相减即可.
解答 解:(1)第n个等式为:2n-2n-1=2n-1,
∵左边=2n-2n-1=2n-1(2-1)=2n-1,
右边=2n-1,
∴左边=右边,
∴2n-2n-1=2n-1,
(2)设a=2°+21+22+23+…+22014+22015.①
则2a=21+22+23+…+22014+22015+22016②
由②-①得:a=22016-1,
∴20+21+22+23+…+22014+22015=22016-1.
点评 本题考查了因式分解的应用,同时也是一个探寻规律问题;此类题要认真观察,善于联想,总结规律,并能正确的应用规律.


科目:初中数学 来源: 题型:选择题
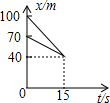 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )
在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )| A. | 喜羊羊与灰太狼最初的距离是30m | |
| B. | 灰太狼用15s追上了喜羊羊 | |
| C. | 灰太狼跑了60m追上了喜羊羊 | |
| D. | 灰太狼追上喜羊羊时,喜羊羊跑了60m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,
已知等边三角形ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连接GD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,折线ABC是某市在2012年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象,观察图象回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费1.4元.
如图,折线ABC是某市在2012年乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象,观察图象回答,乘客在乘车里程超过3千米时,每多行驶1km,要再付费1.4元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com