
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.
(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
【答案】
(1)50
(2)解:如图:

(3)解:根据题意如表:

∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种,
∴P= ![]() ,
,
答:选中一名男生和一名女生的概率为: ![]() .
.
【解析】解:(1)因为合格的男生有2人,女生有1人,共计2+1=3人,
又因为评级合格的学生占6%,
所以全班共有:3÷6%=50(人).
故答案为:50.(2)根据题意得:
女生评级3A的学生是:50×16%﹣3=8﹣3=5(人),
女生评级4A的学生是:50×50%﹣10=25﹣10=15(人),
(2)如图:

(3)根据题意如表:

∵共有12种等可能的结果数,其中一名男生和一名女生的共有7种,
∴P= ![]() ,
,
答:选中一名男生和一名女生的概率为: ![]() .
.
故答案为:(1)50;(2)见解答过程;(3)![]() .
.
(1)先求得合格的总人数为3,然后依据总数=频数÷百分比求解即可;
(2)先求得评级为3A和4A的人数,从而可求得求得评级为3A和4A的女上人数;
(3)先依据列出表格,然后再求得所有可能出现的情况以及恰好一男一女的情况数,最后,利用概率公式求解即可.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人分两次在同一粮店内买粮食,两次的单价不同,甲每次购粮100千克,乙每次购粮100元.若规定:谁两次购粮的平均单价低,谁的购粮方式就合算.那么这两次购粮( )
A. 甲合算 B. 乙合算
C. 甲、乙一样 D. 要看两次的价格情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装360辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练和2名新工人每月可安装12辆电动汽车;2名熟练工和3名新工人每月可安装21辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为( )
A.6cm2
B.8cm2
C.10cm2
D.12cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
科目:初中数学 来源: 题型:
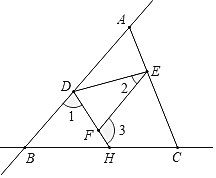
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°.
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=![]() 求∠3的度数(用含
求∠3的度数(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的游艺会上,投飞标游艺区游戏区规则如下,如图投到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点)现统计小华、小明和小芳掷中与得分情况如图所示.

(1)求掷中A区、B区一次各得多少分?
(2)依此方法计算小明的得分为多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题.
材料一:若一个整数m能表示成a2-b2(a,b为整数)的形式,则称这个数为“完美数”.例如,3=22-12,9=32-02,12=42-22,则3,9,12都是“完美数”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整数),所以M也是”完美数”.
材料二:任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)8______(填写“是”或“不是”)一个完美数,F(8)= ______.
(2)如果m和n都是”完美数”,试说明mn也是完美数”.
(3)若一个两位数n的十位数和个位数分别为x,y(1≤x≤9),n为“完美数”且x+y能够被8整除,求F(n)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com